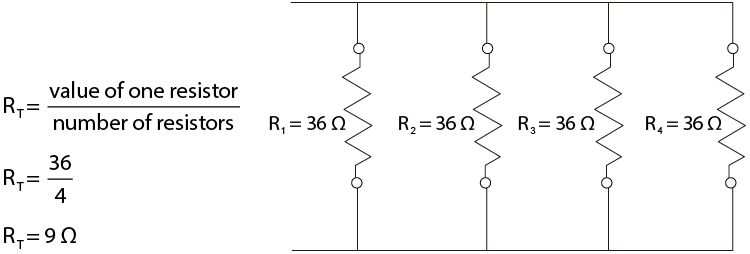
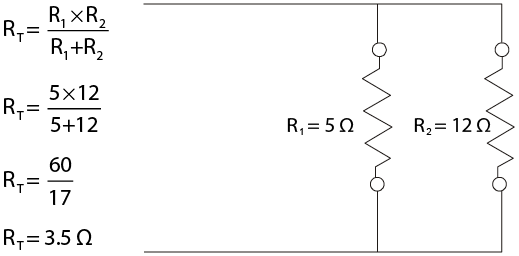
2.3: Parallel Circuits
- Page ID
- 3268
The parallel circuit (Figure \(\PageIndex{1}\)) has completely different characteristics. In a parallel circuit, two or more loads are connected side by side and are controlled by one or more switches. The different loads can each have their own switch, but the major difference is that each of the loads has access to the same amount of voltage and can operate independently of the others. There is more than one path through which the current can flow.

saf
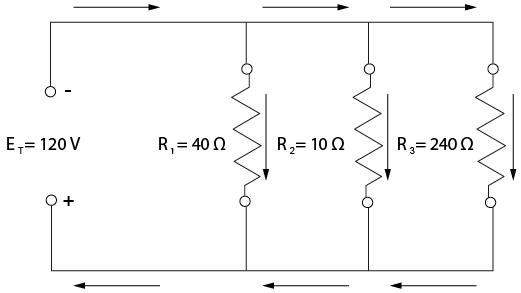
\[\begin{array}{l}{\mathrm{I}_{1}=\frac{\mathrm{E}_{1}}{\mathrm{R}_{1}}=\frac{120}{40}=3 \mathrm{amps}} \\ {\mathrm{I}_{2}=\frac{\mathrm{E}_{2}}{\mathrm{R}_{2}}=\frac{120}{10}=12 \mathrm{amps}} \\ {\mathrm{I}_{3}=\frac{\mathrm{E}_{3}}{\mathrm{R}_{3}}=\frac{120}{240}=0.5 \mathrm{amp}}\end{array}\]
\[R_{T}=\frac{E_{T}}{I_{T}}=\frac{120}{15.5}=7.7 \text { ohms }\]
\[R_{T}=\frac{1}{\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}} \ldots}\]
\[\begin{aligned} R_{T}=& \frac{1}{\frac{1}{40}+\frac{1}{10}+\frac{1}{240}}=7.7 \text { ohms } \\ R_{T}=& \frac{1}{\frac{6}{240}+\frac{24}{240}+\frac{1}{240}} \\ R_{T}=& \frac{\frac{240}{240}}{31} \\ R_{T}=& 7.7 \text { ohms } \end{aligned}\]