4.5: The Common-emitter Amplifier
- Page ID
- 753
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transistor as a Simple Switch
One of the simpler transistor amplifier circuits to study previously illustrated the transistor’s switching ability. (Figure below)
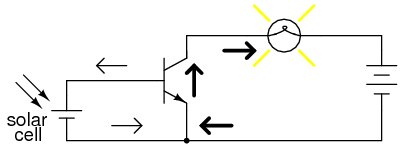
NPN transistor as a simple switch.
It is called the common-emitter configuration because (ignoring the power supply battery) both the signal source and the load share the emitter lead as a common connection point shown in Figure below. This is not the only way in which a transistor may be used as an amplifier, as we will see in later sections of this chapter.
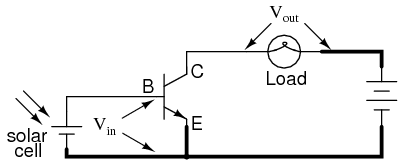
Common-emitter amplifier: The input and output signals both share a connection to the emitter.
Before, a small solar cell current saturated a transistor, illuminating a lamp. Knowing now that transistors are able to “throttle” their collector currents according to the amount of base current supplied by an input signal source, we should see that the brightness of the lamp in this circuit is controllable by the solar cell’s light exposure. When there is just a little light shone on the solar cell, the lamp will glow dimly. The lamp’s brightness will steadily increase as more light falls on the solar cell.
Suppose that we were interested in using the solar cell as a light intensity instrument. We want to measure the intensity of incident light with the solar cell by using its output current to drive a meter movement. It is possible to directly connect a meter movement to a solar cell (Figure below) for this purpose. In fact, the simplest light-exposure meters for photography work are designed like this.
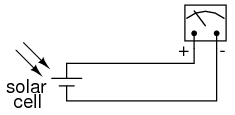
High intensity light directly drives light meter.
Although this approach might work for moderate light intensity measurements, it would not work as well for low light intensity measurements. Because the solar cell has to supply the meter movement’s power needs, the system is necessarily limited in its sensitivity. Supposing that our need here is to measure very low-level light intensities, we are pressed to find another solution.
Transistor as an Amplifier
Perhaps the most direct solution to this measurement problem is to use a transistor (Figure below) to amplify the solar cell’s current so that more meter deflection may be obtained for less incident light.
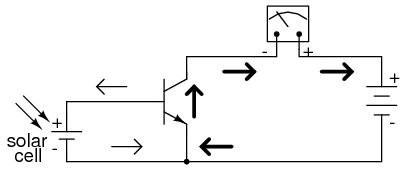
Cell current must be amplified for low intensity light.
Current through the meter movement in this circuit will be β times the solar cell current. With a transistor β of 100, this represents a substantial increase in measurement sensitivity. It is prudent to point out that the additional power to move the meter needle comes from the battery on the far right of the circuit, not the solar cell itself. All the solar cell’s current does is control battery current to the meter to provide a greater meter reading than the solar cell could provide unaided.
Because the transistor is a current-regulating device, and because meter movement indications are based on the current through the movement coil, meter indication in this circuit should depend only on the current from the solar cell, not on the amount of voltage provided by the battery. This means the accuracy of the circuit will be independent of battery condition, a significant feature! All that is required of the battery is a certain minimum voltage and current output ability to drive the meter full-scale.
Voltage Output due to Current Through a Load Resistor
Another way in which the common-emitter configuration may be used is to produce an output voltage derived from the input signal, rather than a specific output current. Let’s replace the meter movement with a plain resistor and measure voltage between collector and emitter in Figure below
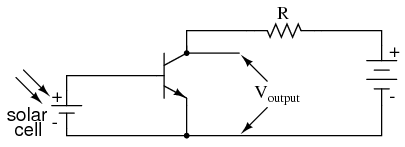
Common emitter amplifier develops voltage output due to current through load resistor.
With the solar cell darkened (no current), the transistor will be in cutoff mode and behave as an open switch between collector and emitter. This will produce maximum voltage drop between collector and emitter for maximum Voutput, equal to the full voltage of the battery.
At full power (maximum light exposure), the solar cell will drive the transistor into saturation mode, making it behave like a closed switch between collector and emitter. The result will be minimum voltage drop between collector and emitter, or almost zero output voltage. In actuality, a saturated transistor can never achieve zero voltage drop between collector and emitter because of the two PN junctions through which collector current must travel. However, this “collector-emitter saturation voltage” will be fairly low, around several tenths of a volt, depending on the specific transistor used.
For light exposure levels somewhere between zero and maximum solar cell output, the transistor will be in its active mode, and the output voltage will be somewhere between zero and full battery voltage. An important quality to note here about the common-emitter configuration is that the output voltage is inverted with respect to the input signal. That is, the output voltage decreases as the input signal increases. For this reason, the common-emitter amplifier configuration is referred to as an inverting amplifier.
A quick SPICE simulation (Figure below) of the circuit in Figure below will verify our qualitative conclusions about this amplifier circuit.
Common emitter schematic with node numbers and corresponding SPICE netlist.
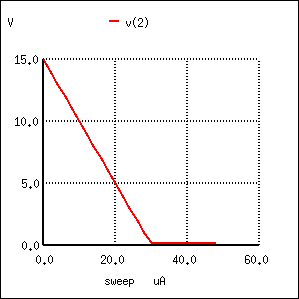
Common emitter: collector voltage output vs base current input.
At the beginning of the simulation in Figure above where the current source (solar cell) is outputting zero current, the transistor is in cutoff mode and the full 15 volts from the battery is shown at the amplifier output (between nodes 2 and 0). As the solar cell’s current begins to increase, the output voltage proportionally decreases, until the transistor reaches saturation at 30 µA of base current (3 mA of collector current). Notice how the output voltage trace on the graph is perfectly linear (1 volt steps from 15 volts to 1 volt) until the point of saturation, where it never quite reaches zero. This is the effect mentioned earlier, where a saturated transistor can never achieve exactly zero voltage drop between collector and emitter due to internal junction effects. What we do see is a sharp output voltage decrease from 1 volt to 0.2261 volts as the input current increases from 28 µA to 30 µA, and then a continuing decrease in output voltage from then on (albeit in progressively smaller steps). The lowest the output voltage ever gets in this simulation is 0.1299 volts, asymptotically approaching zero.
Transistor as an AC Amplifier
So far, we’ve seen the transistor used as an amplifier for DC signals. In the solar cell light meter example, we were interested in amplifying the DC output of the solar cell to drive a DC meter movement, or to produce a DC output voltage. However, this is not the only way in which a transistor may be employed as an amplifier. Often an AC amplifier for amplifying alternating current and voltage signals is desired. One common application of this is in audio electronics (radios, televisions, and public-address systems). Earlier, we saw an example of the audio output of a tuning fork activating a transistor switch. (Figure below) Let’s see if we can modify that circuit to send power to a speaker rather than to a lamp in Figure below.
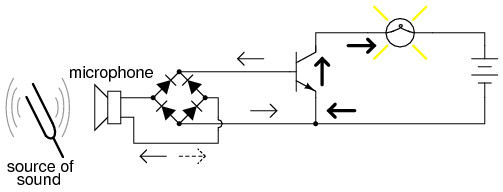
Transistor switch activated by audio.
In the original circuit, a full-wave bridge rectifier was used to convert the microphone’s AC output signal into a DC voltage to drive the input of the transistor. All we cared about here was turning the lamp on with a sound signal from the microphone, and this arrangement sufficed for that purpose. But now we want to actually reproduce the AC signal and drive a speaker. This means we cannot rectify the microphone’s output anymore, because we need undistorted AC signal to drive the transistor! Let’s remove the bridge rectifier and replace the lamp with a speaker:
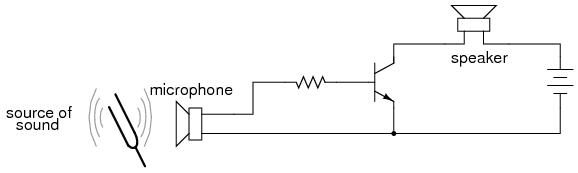
Common emitter amplifier drives speaker with audio frequency signal.
Since the microphone may produce voltages exceeding the forward voltage drop of the base-emitter PN (diode) junction, I’ve placed a resistor in series with the microphone. Let’s simulate the circuit in Figure below with SPICE. The netlist is included in (Figure below)
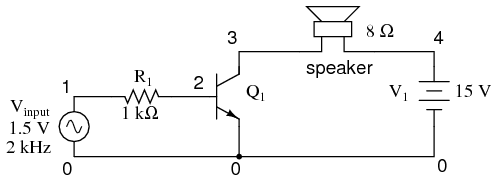
SPICE version of common emitter audio amplifier.
Signal clipped at collector due to lack of DC base bias.
The simulation plots (Figure above) both the input voltage (an AC signal of 1.5 volt peak amplitude and 2000 Hz frequency) and the current through the 15 volt battery, which is the same as the current through the speaker. What we see here is a full AC sine wave alternating in both positive and negative directions, and a half-wave output current waveform that only pulses in one direction. If we were actually driving a speaker with this waveform, the sound produced would be horribly distorted.
What’s wrong with the circuit? Why won’t it faithfully reproduce the entire AC waveform from the microphone? The answer to this question is found by close inspection of the transistor diode current source model in Figure below.
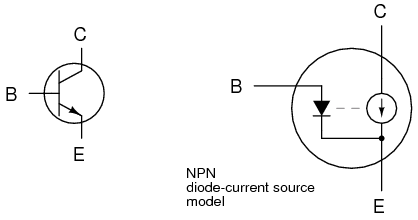
The model shows that base current flow in on direction.
Collector current is controlled, or regulated, through the constant-current mechanism according to the pace set by the current through the base-emitter diode. Note that both current paths through the transistor are monodirectional: one way only! Despite our intent to use the transistor to amplify an AC signal, it is essentially a DC device, capable of handling currents in a single direction. We may apply an AC voltage input signal between the base and emitter, but electrons cannot flow in that circuit during the part of the cycle that reverse-biases the base-emitter diode junction. Therefore, the transistor will remain in cutoff mode throughout that portion of the cycle. It will “turn on” in its active mode only when the input voltage is of the correct polarity to forward-bias the base-emitter diode, and only when that voltage is sufficiently high to overcome the diode’s forward voltage drop. Remember that bipolar transistors are current-controlled devices: they regulate collector current based on the existence of base-to-emitter current, not base-to-emitter voltage.
The only way we can get the transistor to reproduce the entire waveform as current through the speaker is to keep the transistor in its active mode the entire time. This means we must maintain current through the base during the entire input waveform cycle. Consequently, the base-emitter diode junction must be kept forward-biased at all times. Fortunately, this can be accomplished with a DC bias voltage added to the input signal. By connecting a sufficient DC voltage in series with the AC signal source, forward-bias can be maintained at all points throughout the wave cycle. (Figure below)
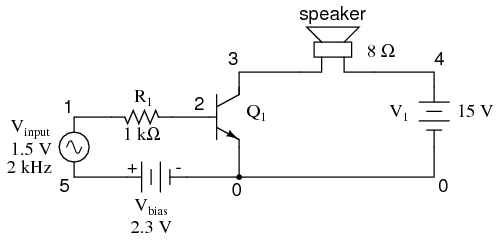
Vbias keeps transistor in the active region.
Undistorted output current I(v(1) due to Vbias
With the bias voltage source of 2.3 volts in place, the transistor remains in its active mode throughout the entire cycle of the wave, faithfully reproducing the waveform at the speaker. (Figure above) Notice that the input voltage (measured between nodes 1 and 0) fluctuates between about 0.8 volts and 3.8 volts, a peak-to-peak voltage of 3 volts just as expected (source voltage = 1.5 volts peak). The output (speaker) current varies between zero and almost 300 mA, 180o out of phase with the input (microphone) signal.
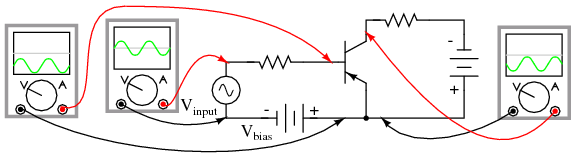
The illustration in Figure below is another view of the same circuit, this time with a few oscilloscopes (“scopemeters”) connected at crucial points to display all the pertinent signals.
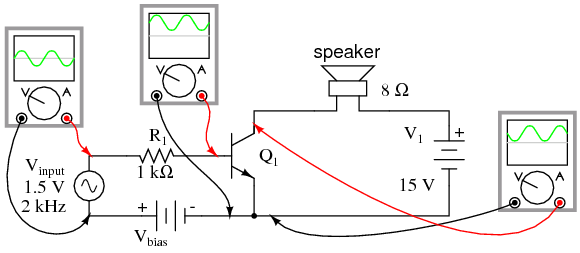
Input is biased upward at base. Output is inverted.
Biasing
The need for biasing a transistor amplifier circuit to obtain full waveform reproduction is an important consideration. A separate section of this chapter will be devoted entirely to the subject biasing and biasing techniques. For now, it is enough to understand that biasing may be necessary for proper voltage and current output from the amplifier.
Now that we have a functioning amplifier circuit, we can investigate its voltage, current, and power gains. The generic transistor used in these SPICE analyses has a β of 100, as indicated by the short transistor statistics printout included in the text output in Table below (these statistics were cut from the last two analyses for brevity’s sake).
β is listed under the abbreviation “bf,” which actually stands for “beta, forward”. If we wanted to insert our own β ratio for an analysis, we could have done so on the .model line of the SPICE netlist.
Since β is the ratio of collector current to base current, and we have our load connected in series with the collector terminal of the transistor and our source connected in series with the base, the ratio of output current to input current is equal to beta. Thus, our current gain for this example amplifier is 100, or 40 dB.
Voltage gain is a little more complicated to figure than current gain for this circuit. As always, voltage gain is defined as the ratio of output voltage divided by input voltage. In order to experimentally determine this, we modify our last SPICE analysis to plot output voltage rather than output current so we have two voltage plots to compare in Figure below.
Plotted on the same scale (from 0 to 4 volts), we see that the output waveform in Figure above has a smaller peak-to-peak amplitude than the input waveform , in addition to being at a lower bias voltage, not elevated up from 0 volts like the input. Since voltage gain for an AC amplifier is defined by the ratio of AC amplitudes, we can ignore any DC bias separating the two waveforms. Even so, the input waveform is still larger than the output, which tells us that the voltage gain is less than 1 (a negative dB figure).
To be honest, this low voltage gain is not characteristic to all common-emitter amplifiers. It is a consequence of the great disparity between the input and load resistances. Our input resistance (R1) here is 1000 Ω, while the load (speaker) is only 8 Ω. Because the current gain of this amplifier is determined solely by the β of the transistor, and because that β figure is fixed, the current gain for this amplifier won’t change with variations in either of these resistances. However, voltage gain is dependent on these resistances. If we alter the load resistance, making it a larger value, it will drop a proportionately greater voltage for its range of load currents, resulting in a larger output waveform. Let’s try another simulation, only this time with a 30 Ω in Figure below load instead of an 8 Ω load.
This time the output voltage waveform in Figure above is significantly greater in amplitude than the input waveform. Looking closely, we can see that the output waveform crests between 0 and about 9 volts: approximately 3 times the amplitude of the input voltage.
We can do another computer analysis of this circuit, this time instructing SPICE to analyze it from an AC point of view, giving us peak voltage figures for input and output instead of a time-based plot of the waveforms. (Table below)
Peak voltage measurements of input and output show an input of 1.5 volts and an output of 4.418 volts. This gives us a voltage gain ratio of 2.9453 (4.418 V / 1.5 V), or 9.3827dB.
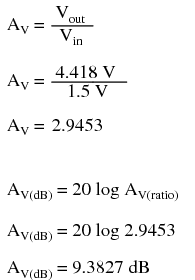
Because the current gain of the common-emitter amplifier is fixed by β, and since the input and output voltages will be equal to the input and output currents multiplied by their respective resistors, we can derive an equation for approximate voltage gain:
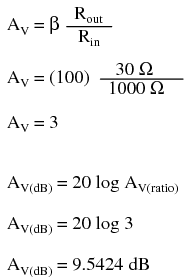
As you can see, the predicted results for voltage gain are quite close to the simulated results. With perfectly linear transistor behavior, the two sets of figures would exactly match. SPICE does a reasonable job of accounting for the many “quirks” of bipolar transistor function in its analysis, hence the slight mismatch in voltage gain based on SPICE’s output.
These voltage gains remain the same regardless of where we measure output voltage in the circuit: across collector and emitter, or across the series load resistor as we did in the last analysis. The amount of output voltage change for any given amount of input voltage will remain the same. Consider the two following SPICE analyses as proof of this. The first simulation in Figure below is time-based, to provide a plot of input and output voltages. You will notice that the two signals are 180o out of phase with each other. The second simulation in Table below is an AC analysis, to provide simple, peak voltage readings for input and output.
We still have a peak output voltage of 4.418 volts with a peak input voltage of 1.5 volts. The only difference from the last set of simulations is the phase of the output voltage.
So far, the example circuits shown in this section have all used NPN transistors. PNP transistors are just as valid to use as NPN in any amplifier configuration, as long as the proper polarity and current directions are maintained, and the common-emitter amplifier is no exception. The output invertion and gain of a PNP transistor amplifier are the same as its NPN counterpart, just the battery polarities are different. (Figure below)
PNP version of common emitter amplifier.
Review
- Common-emitter transistor amplifiers are so-called because the input and output voltage points share the emitter lead of the transistor in common with each other, not considering any power supplies.
- Transistors are essentially DC devices: they cannot directly handle voltages or currents that reverse direction. To make them work for amplifying AC signals, the input signal must be offset with a DC voltage to keep the transistor in its active mode throughout the entire cycle of the wave. This is called biasing.
- If the output voltage is measured between emitter and collector on a common-emitter amplifier, it will be 180o out of phase with the input voltage waveform. Thus, the common-emitter amplifier is called an inverting amplifier circuit.
- The current gain of a common-emitter transistor amplifier with the load connected in series with the collector is equal to β. The voltage gain of a common-emitter transistor amplifier is approximately given here:
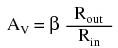
- Where “Rout” is the resistor connected in series with the collector and “Rin” is the resistor connected in series with the base.


