4.16: BJT Quirks
- Page ID
- 1801
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An ideal transistor would show 0% distortion in amplifying a signal. Its gain would extend to all frequencies. It would control hundreds of amperes of current, at hundreds of degrees C. In practice, available devices show distortion. Amplification is limited at the high frequency end of the spectrum. Real parts only handle tens of amperes with precautions. Care must be taken when paralleling transistors for higher current. Operation at elevated temperatures can destroy transistors if precautions are not taken.
Nonlinearity
The class A common-emitter amplifier (similar to Figure previous)is driven almost to clipping in Figure below. Note that the positive peak is flatter than the negative peaks. This distortion is unacceptable in many applications like high-fidelity audio.
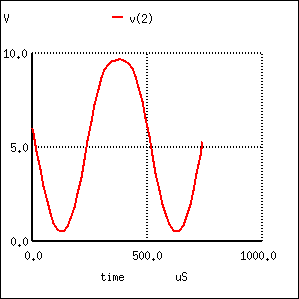
Distortion in large signal common-emitter amplifier.
Small signal amplifiers are relatively linear because they use a small linear section of the transistor characteristics. Large signal amplifiers are not 100% linear because transistor characteristics like β are not constant, but vary with collector current. β is high at low collector current, and low at very low current or high current. Though, we primarily encounter decreasing β with increasing collector current.
SPICE net list: for transient and fourier analyses. Fourier analysis shows 10% total harmonic distortion (THD).
The SPICE listing in Table above illustrates how to quantify the amount of distortion. The “.fourier 2000 v(2)” command tells SPICE to perm a fourier analysis at 2000 Hz on the output v(2). At the command line “spice -b circuitname.cir” produces the Fourier analysis output in Table above. It shows THD (total harmonic distortion) of over 10%, and the contribution of the individual harmonics.
A partial solution to this distortion is to decrease the collector current or operate the amplifier over a smaller portion of the load line. The ultimate solution is to apply negative feedback. See Feedback.
Temperature drift
Temperature affects the AC and DC characteristics of transistors. The two aspects to this problem are environmental temperature variation and self-heating. Some applications, like military and automotive, require operation over an extended temperature range. Circuits in a benign environment are subject to self-heating, in particular high power circuits.
Leakage current ICO and β increase with temperature. The DC β hFE increases exponentially. The AC β hfeincreases, but not as rapidly. It doubles over the range of -55o to 85o C. As temperature increases, the increase in hfe will yield a larger common-emitter output, which could be clipped in extreme cases. The increase in hFE shifts the bias point, possibly clipping one peak. The shift in bias point is amplified in multi-stage direct-coupled amplifiers. The solution is some form of negative feedback to stabilize the bias point. This also stabilizes AC gain.
Increasing temperature in Figure below (a) will decrease VBE from the nominal 0.7V for silicon transistors. Decreasing VBE increases collector current in a common-emitter amplifier, further shifting the bias point. The cure for shifting VBE is a pair of transistors configured as a differential amplifier. If both transistors in Figurebelow (b) are at the same temperature, the VBE will track with changing temperature and cancel.
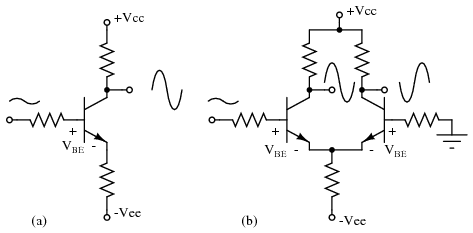
(a) single ended CE amplifier vs (b) differential amplifier with VBE cancellation.
The maximum recommended junction temperature for silicon devices is frequently 125o C. Though, this should be derated for higher reliability. Transistor action ceases beyond 150o C. Silicon carbide and diamond transistors will operate considerably higher.
Thermal runaway
The problem with increasing temperature causing increasing collector current is that more current increase the power dissipated by the transistor which, in turn, increases its temperature. This self-reinforcing cycle is known as thermal run away, which may destroy the transistor. Again, the solution is a bias scheme with some form of negative feedback to stabilize the bias point.
Junction capacitance
Capacitance exists between the terminals of a transistor. The collector-base capacitance CCB and emitter-base capacitance CEB decrease the gain of a common emitter circuit at higher frequencies.
In a common emitter amplifier, the capacitive feedback from collector to base effectively multiplies CCB by β. The amount of negative gain-reducing feedback is related to both current gain, and amount of collector-base capacitance. This is known as the Miller effect.
Noise
The ultimate sensitivity of small signal amplifiers is limited by noise due to random variations in current flow. The two major sources of noise in transistors are shot noise due to current flow of carriers in the base and thermal noise. The source of thermal noise is device resistance and increases with temperature:

Noise in a transistor amplifier is defined in terms of excess noise generated by the amplifier, not that noise amplified from input to output, but that generated within the amplifier. This is determined by measuring the signal to noise ratio (S/N) at the amplifier input and output. The AC voltage output of an amplifier with a small signal input corresponds to S+N, signal plus noise. The AC voltage with no signal in corresponds to noise N. The noise figure F is defined in terms of S/N of amplifier input and output:
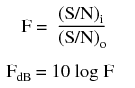
The noise figure F for RF (radio frequency) transistors is usually listed on transistor data sheets in decibels, FdB. A good VHF (very high frequency, 30 MHz to 300 Mhz) noise figure is < 1 dB. The noise figure above VHF increases considerable, 20 dB per decade as shown in Figure below.
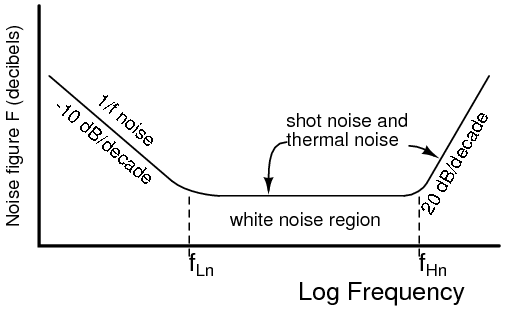
Small signal transistor noise figure vs Frequency. After Thiele, Figure 11.147 [AGT]
Figure above also shows that noise at low frequencies increases at 10 dB per decade with decreasing frequency. This noise is known as 1/f noise.
Noise figure varies with the transistor type (part number). Small signal RF transistors used at the antenna input of a radio receiver are specifically designed for low noise figure. Noise figure varies with bias current and impedance matching. The best noise figure for a transistor is achieved at lower bias current, and possibly with an impedance mismatch.
Thermal mismatch (problem with paralleling transistors)
If two identical power transistors were paralleled for higher current, one would expect them to share current equally. Because of differences in characteristerics, transistors do not share current equally.
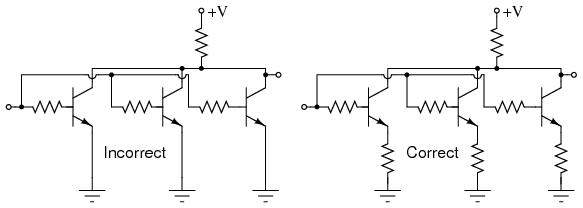
Transistors paralleled for increased power require emitter ballast resistors
It is not practical to select identical transistors. The β for small signal transistors typically has a range of 100-300, power transistors: 20-50. If each one could be matched, one still might run hotter than the other due to environmental conditions. The hotter transistor draws more current resulting in thermal runaway. The solution when paralleling bipolar transistors is to insert emitter resistors known as ballast resistors of less than an ohm. If the hotter transistor draws more current, the voltage drop across the ballast resistor increases— negative feedback. This decreases the current. Mounting all transistors on the same heatsink helps equalize current too.
High frequency effects
The performance of a transistor amplifier is relatively constant, up to a point, as shown by the small signal common-emitter current gain with increasing frequency in Figure below. Beyond that point the performance of a transistor degrades as frequency increases.
Beta cutoff frequency, fT is the frequency at which common-emitter small signal current gain (hfe) falls to unity. (Figure below) A practical amplifier must have a gain >1. Thus, a transistor cannot be used in a practical amplifier at fT. A more usable limit for a transistor is 0.1·fT.
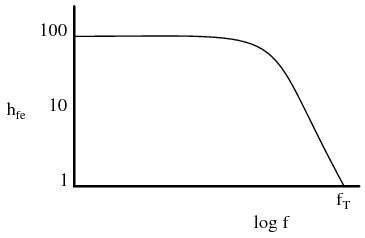
Common-emitter small signal current gain (hfe) vs frequency.
Some RF silicon bipolar transistors are usable as amplifers up to a few GHz. Silicon-germanium devices extend the upper range to 10 GHz.
Alpha cutoff frequency, falpha is the frequency at which the α falls to 0.707 of low frequency α,0 α=0.707α0. Alpha cutoff and beta cutoff are nearly equal: falpha≅fT Beta cutoff fT is the preferred figure of merit of high frequency performance.
fmax is the highest frequency of oscillation possible under the most favorable conditions of bias and impedance matching. It is the frequency at which the power gain is unity. All of the output is fed back to the input to sustain oscillations. fmax is an upper limit for frequency of operation of a transistor as an active device. Though, a practical amplifier would not be usable at fmax.
Miller effect: The high frequency limit for a transistor is related to the junction capacitances. For example a PN2222A has an input capacitance Cobo=9pF and an output capacitance Cibo=25pF from C-B and E-B respectively. [FAR] Although the C-E capacitance of 25 pF seems large, it is less of a factor than the C-B (9pF) capacitance. because of the Miller effect, the C-B capacitance has an effect on the base equivalent to beta times the capacitance in the common-emitter amplifier. Why might this be? A common-emitter amplifier inverts the signal from base to collector. The inverted collector signal fed back to the base opposes the input on the base. The collector signal is beta times larger than the input. For the PN2222A, β=50–300. Thus, the 9pF C-E capacitance looks like 9·50=450pF to 9·300=2700pF.
The solution to the junction capacitance problem is to select a high frequency transistor for wide bandwidth applications— RF (radio frequency) or microwave transistor. The bandwidth can be extended further by using the common-base instead of the common-emitter configuration. The grounded base shields the emitter input from capacitive collector feedback. A two-transistor cascode arrangement will yield the same bandwidth as the common-base, with the higher input impedance of the common-emitter.
Review
- Transistor amplifiers exhibit distortion because of β variation with collector current.
- Ic, VBE, β and junction capacitance vary with temperature.
- An increase in temperature can cause an increase in IC, causing an increase in temperature, a vicious cycle known as thermal runaway.
- Junction capacitance limits high frequency gain of a transistor. The Miller effect makes Ccb look β times larger at the base of a CE amplifier.
- Transistor noise limits the ability to amplify small signals. Noise figure is a figure of merit concerning transistor noise.
- When paralleling power transistors for increased current, insert ballast resistors in series with the emitters to equalize current.
- FT is the absolute upper frequency limit for a CE amplifier, small signal current gain falls to unity, hfe=1.
- Fmax is the upper frequency limit for an oscillator under the most ideal conditions.


