8.1: Introduction to Operational Amplifiers (Op-amps)
- Page ID
- 777
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What is an Operation Amplifier(Op-amp)?
Operational Amplifiers, also known as Op-amps, are basically a voltage amplifying device designed to be used with components like capacitors and resistors, between its in/out terminals. They are essentially a core part of analog devices. Feedback components like these are used to determine the operation of the amplifier. The amplifier can perform many different operations (resistive, capacitive, or both), Giving it the name Operational Amplifier.
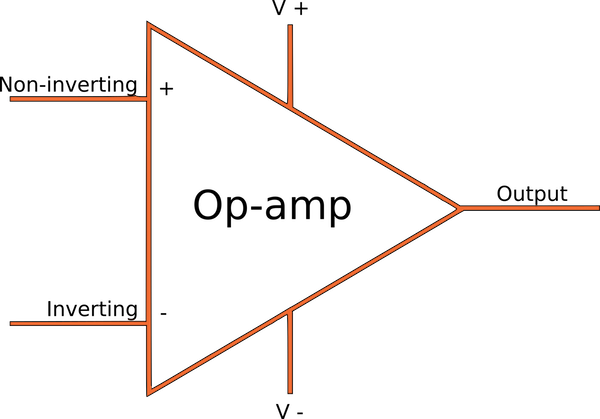
Example of an Op-amp in schematics.
Op-amps are linear devices that are ideal for DC amplification and are used often in signal conditioning, filtering or other mathematical operations (add, subtract, integration and differentiation).
The operational amplifier is arguably the most useful single device in analog electronic circuitry. With only a handful of external components, it can be made to perform a wide variety of analog signal processing tasks. It is also quite affordable, most general-purpose amplifiers selling for under a dollar apiece. Modern designs have been engineered with durability in mind as well: several “op-amps” are manufactured that can sustain direct short-circuits on their outputs without damage.
One key to the usefulness of these little circuits is in the engineering principle of feedback, particularly negative feedback, which constitutes the foundation of almost all automatic control processes. The principles presented in this section, extend well beyond the immediate scope of electronics. It is well worth the electronics student’s time to learn these principles and learn them well.
Further Reading
Operational amplifiers, or opamps, are one of the most fundamental building blocks an electrical engineer can employ in circuit designs. There are a ton of useful applications for opamps. This article will go over just a few basic circuits you can implement in your designs!
The Basics: Voltage Followers
The first circuit is so simple that it almost looks a little crazy:
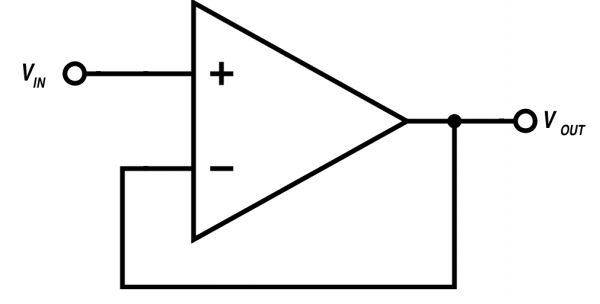
Figure 1: Voltage Follower
This circuit is referred to as a voltage follower, and it behaves like this:
Vin=VoutVin=Vout
On face, this isn't super useful. Why would I pay a few extra cents for an opamp when it looks like a wire would do the same job between two components? The answer is simple once you know a few simple things about opamps. When you start to break down a circuit with opamps, two basic principles should be at the forefront of your mind:
- The opamp's input terminals, V+ and V-, draw no current.
- The voltage of V+ and V- are always equal. This property is sometimes called the virtual short approximation.
Looking at the first rule, we can see that our voltage follower circuit is not drawing any current at the input terminal connected to V+. This is really just a way of saying that V+ has a really high impedance - in fact, since we're talking about ideal opamps, we tend to just say that it has infinite input impedance. In practice, this has some pretty neat implications: if V+ isn't drawing any current, then it means that we could connect Vin to any node in any circuit and measure it without modifying the original circuit. We wouldn't have to go through the tedious rigamarole of solving a bunch of new equations for node voltages and mesh currents, because we wouldn't be disturbing either of them by adding a voltage follower. Pretty cool, huh?
(Note: Like most rules, there are some exceptions to these opamp rules. For the duration of this article, we're going to ignore these exceptions - they would get in the way of analyzing our voltage follower.)
Instead of taking a direct measurement at Vin in our hyptothetical circuit, we'd measure instead at Vout. This is the second rule of opamps in effect - the voltages of V+ and V- are always considered to be equal. Since we've connected V- and and the opamp's output, we can extend this a step further, and say that Vout = V- = V+ due to the virtual short approximation.
Using voltage followers provides a really easy way to interface different circuits that have different impedances. Cool! What else can we do with opamps?
Changing Gain - An Inverting Amplifier
As their name suggests, opamps are amplifiers. They can amplify signals by a certain ratio of input to output. This ratio is commonly referred to as the gain of an operational amplifier. In a perfect world, an opamp's gain would be infinite - so high that it could amplify any signal level to any other signal level. This isn't the case in the real world, but we'll consider it a fact while we analyze the next circuit: an inverting amplifier.
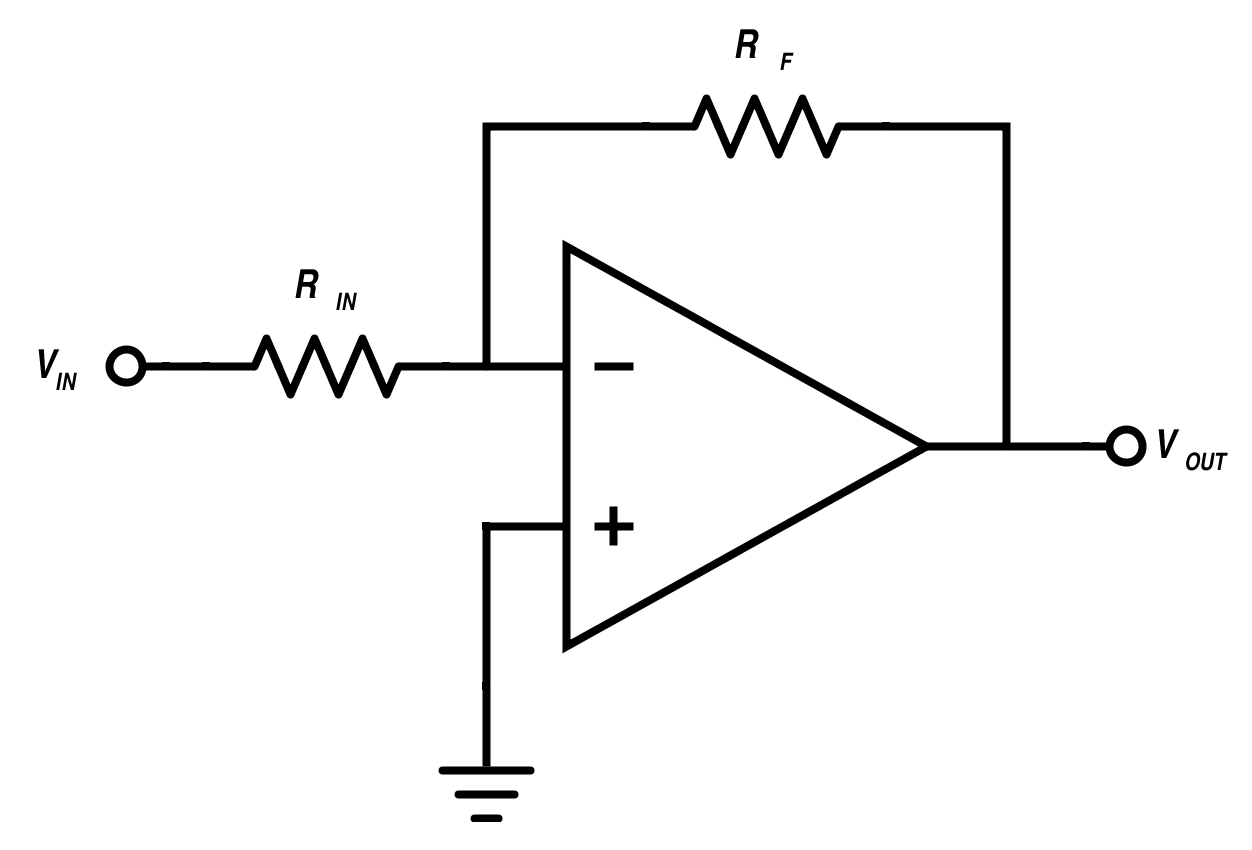.png?revision=1)
Figure 2: Inverting Amplifier
Let's walk through this circuit's operation step by step. First, let's apply our two opamp rules to figure out some node voltages of this circuit. The simplest one to apply is the virtual short approximation, where V+ and V- are always at the same voltage. We can see that V+ is tied to ground; therefore, V- must also be at ground. What about the current going into and out of node V-? By Kirchoff's current law, we know that the sum of all currents at that node must be as follows:
Initially, this looks like it might take some work to solve, as this equation has three unknowns. But does it? If you recall the opamp rules stated earlier, you'll see that we get one term of this equation for free: opamp inputs don't draw any current! Therefore, we know that iV- is equal to zero. We can then rearrange that equation into the following form:
Since V- is tied to ground by the virtual short, Ohm's law allows us to substitute out these currents as voltages and resistances:
Which, with a little algebra, gets us back to where we started:
It's pretty clear why this circuit is useful - it allows you to apply a linear gain to an input and output by choosing (Rf/Rin) to form any ratio you want. The circuit also has the added bonus of allowing you a lot of control over its input impedance - since you're free to choose the resistor value of Rin, you can crank it up as high or as low as needed to fit whatever output impedance you need to match it to!
Why do we need a resistor network to achieve this behavior? To understand that, we'll have to understand a little bit more of how an opamp works. An opamp is a type of voltage amplifier. In the ideal case, an opamp provides infinite gain - it can amplify any voltage to any other voltage level. We can scale the opamp's infinte gain by using a resistor network that connects the input node, V-, and the output node. By connecting the opamp output to an input, we're using a process called _feedback_ to adjust the output voltage to a desired level. Feedback is a really important EE concept, and complex enough to warrant a whole article dedicated to the topic. For now, it's enough to understand the basic principle as it applies to opamps: by connecting the output to an input, you can modify a circuit's behavior in really useful ways.
An Inverse of an Inverter?
Let's see what happens when we start fooling around with the basic inverting amplifier design. What happens if we swap out the feedback network to the other input pin, V-?
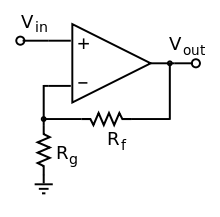
Figure 3: What does this circuit do?
We can go through the same series of steps as we did before with the inverting amplifier, but we start substituting in voltages at the V- node. Due to the virtual short approximation, V- = V+ = Vin. As a result, we can write the following equation for the current going through Rg:
Since we know that the opamp isn't drawing any current, we know that the current through Rg and Rf must be equal, which allows us to write this equation:
The virtual short approximation lets us get rid of V-, since we know it is equal to Vin.
And with a bit of algebraic rearranging, we get the following:
Unlike the previous circuit, the gain of this circuit is nonnegative. As a result, this circuit is called a noninverting amplifier: It provides a linear gain, but with a positive sign. Unlike the previous noninverting amplifier, it cannot provide any gain less than unity - it's impossible to set the feedback network any lower! On the other hand, this circuit does provide one thing that the inverting amplifier does not. Since the output is positive, it is in phase with the input. The inverting amplifier, by virtue of applying a negative gain, is shifting the output signal by 180 degrees. The noninverting amplifier doesn't do this!
Wrapping Up
Opamps are really versatile circuit components. This article barely scratches the surface of what can be done with them - the range of functionality that they can bring to bear is enormous. What are some of the other circuits you can make with them? Have any cool circuits you've built with opamps? Leave us a note in the comment section and tell us about it!


