4.4: Contact “Bounce”
- Page ID
- 912
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When a switch is actuated and contacts touch one another under the force of actuation, they are supposed to establish continuity in a single, crisp moment. Unfortunately, though, switches do not exactly achieve this goal. Due to the mass of the moving contact and any elasticity inherent in the mechanism and/or contact materials, contacts will “bounce” upon closure for a period of milliseconds before coming to a full rest and providing unbroken contact. In many applications, switch bounce is of no consequence: it matters little if a switch controlling an incandescent lamp “bounces” for a few cycles every time it is actuated. Since the lamp’s warm-up time greatly exceeds the bounce period, no irregularity in lamp operation will result.
However, if the switch is used to send a signal to an electronic amplifier or some other circuit with a fast response time, contact bounce may produce very noticeable and undesired effects:
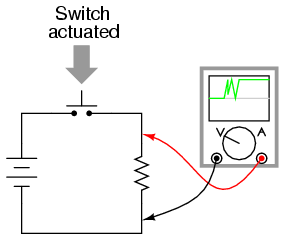
A closer look at the oscilloscope display reveals a rather ugly set of makes and breaks when the switch is actuated a single time:
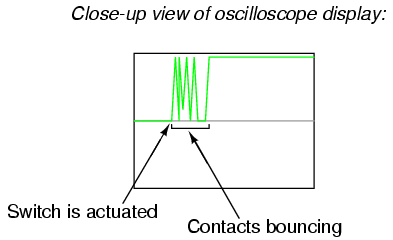
If, for example, this switch is used to provide a “clock” signal to a digital counter circuit, so that each actuation of the pushbutton switch is supposed to increment the counter by a value of 1, what will happen instead is the counter will increment by several counts each time the switch is actuated. Since mechanical switches often interface with digital electronic circuits in modern systems, switch contact bounce is a frequent design consideration. Somehow, the “chattering” produced by bouncing contacts must be eliminated so that the receiving circuit sees a clean, crisp off/on transition:
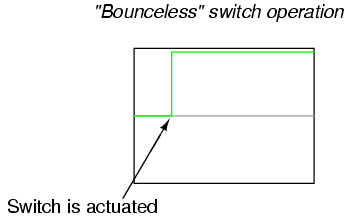
Switch contacts may be debounced several different ways. The most direct means is to address the problem at its source: the switch itself. Here are some suggestions for designing switch mechanisms for minimum bounce:
- Reduce the kinetic energy of the moving contact. This will reduce the force of impact as it comes to rest on the stationary contact, thus minimizing bounce.
- Use “buffer springs” on the stationary contact(s) so that they are free to recoil and gently absorb the force of impact from the moving contact.
- Design the switch for “wiping” or “sliding” contact rather than direct impact. “Knife” switch designs use sliding contacts.
- Dampen the switch mechanism’s movement using an air or oil “shock absorber” mechanism.
- Use sets of contacts in parallel with each other, each slightly different in mass or contact gap, so that when one is rebounding off the stationary contact, at least one of the others will still be in firm contact.
- “Wet” the contacts with liquid mercury in a sealed environment. After initial contact is made, the surface tension of the mercury will maintain circuit continuity even though the moving contact may bounce off the stationary contact several times.
Each one of these suggestions sacrifices some aspect of switch performance for limited bounce, and so it is impractical to design all switches with limited contact bounce in mind. Alterations made to reduce the kinetic energy of the contact may result in a small open-contact gap or a slow-moving contact, which limits the amount of voltage the switch may handle and the amount of current it may interrupt. Sliding contacts, while non-bouncing, still produce “noise” (irregular current caused by irregular contact resistance when moving), and suffer from more mechanical wear than normal contacts.
Multiple, parallel contacts give less bounce, but only at greater switch complexity and cost. Using mercury to “wet” the contacts is a very effective means of bounce mitigation, but it is unfortunately limited to switch contacts of low ampacity. Also, mercury-wetted contacts are usually limited in mounting position, as gravity may cause the contacts to “bridge” accidently if oriented the wrong way.
If re-designing the switch mechanism is not an option, mechanical switch contacts may be debounced externally, using other circuit components to condition the signal. A low-pass filter circuit attached to the output of the switch, for example, will reduce the voltage/current fluctuations generated by contact bounce:
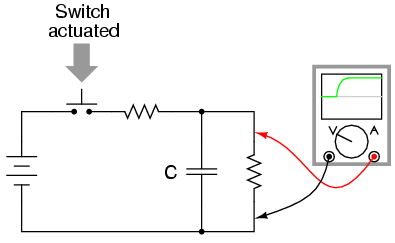
Switch contacts may be debounced electronically, using hysteretic transistor circuits (circuits that “latch” in either a high or a low state) with built-in time delays (called “one-shot” circuits), or two inputs controlled by a double-throw switch. These hysteretic circuits, called multivibrators, are discussed in detail in a later chapter.


