3.4: Voltage Divider
- Page ID
- 1253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- Calculator (or pencil and paper for doing arithmetic)
- 6-volt battery
- Assortment of resistors between 1 KΩ and 100 kΩ in value
I’m purposely restricting the resistance values between 1 kΩ and 100 kΩ for the sake of obtaining accurate voltage and current readings with your meter. With very low resistance values, the internal resistance of the ammeter has a significant impact on measurement accuracy. Very high resistance values may cause problems for voltage measurement, the internal resistance of the voltmeter substantially changing circuit resistance when it is connected in parallel with a high-value resistor.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 1, chapter 6: “Divider Circuits and Kirchhoff’s Laws”
LEARNING OBJECTIVES
- Voltmeter use
- Ammeter use
- Ohmmeter use
- Use of Ohm’s Law
- Use of Kirchhoff’s Voltage Law (“KVL”)
- Voltage divider design
SCHEMATIC DIAGRAM
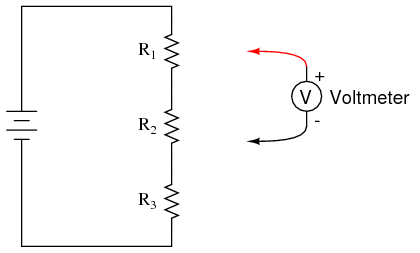
ILLUSTRATION
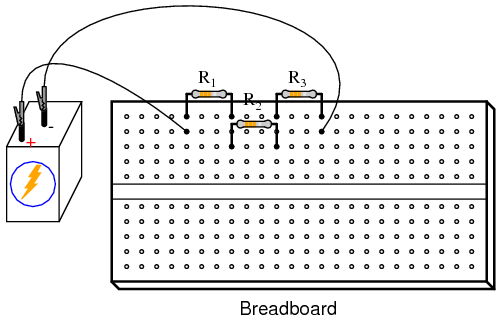
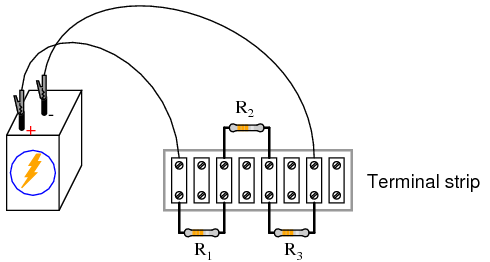
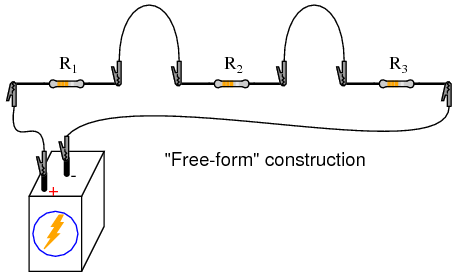
INSTRUCTIONS
Shown here are three different methods of circuit construction: on a breadboard, on a terminal strip, and “free-form.” Try building the same circuit each way to familiarize yourself with the different construction techniques and their respective merits. The “free-form” method—where all components are connected together with “alligator-” style jumper wires—is the least professional, but appropriate for a simple experiment such as this. Breadboard construction is versatile and allows for high component density (many parts in a small space), but is quite temporary. Terminal strips offer a much more permanent form of construction at the cost of low component density.
Select three resistors from your resistor assortment and measure the resistance of each one with an ohmmeter. Note these resistance values with pen and paper, for reference in your circuit calculations.
Connect the three resistors in series, and to the 6-volt battery, as shown in the illustrations. Measure battery voltage with a voltmeter after the resistors have been connected to it, noting this voltage figure on paper as well. It is advisable to measure battery voltage while its powering the resistor circuit because this voltage may differ slightly from a no-load condition. We saw this effect exaggerated in the “parallel battery” experiment while powering a high-wattage lamp: battery voltage tends to “sag” or “droop” under load. Although this three-resistor circuit should not present a heavy enough load (not enough current drawn) to cause significant voltage “sag,” measuring battery voltage under load is a good scientific practice because it provides more realistic data.
Use Ohm’s Law (I=E/R) to calculate circuit current, then verify this calculated value by measuring current with an ammeter like this (“terminal strip” version of the circuit shown as an arbitrary choice in construction method):
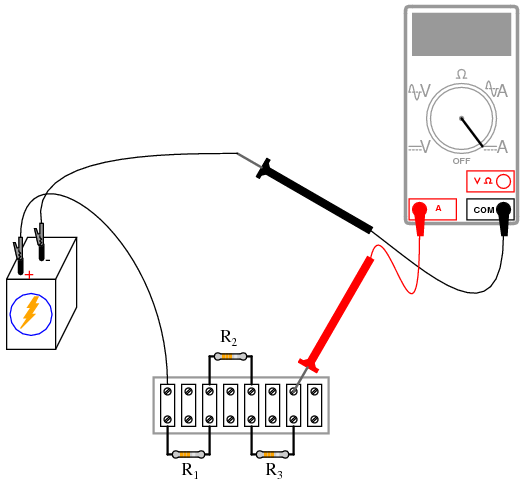
If your resistor values are indeed between 1 kΩ and 100 kΩ, and the battery voltage approximately 6 volts, the current should be a very small value, in the milliamp (mA) or microamp (µA) range. When you measure current with a digital meter, the meter may show the appropriate metric prefix symbol (m or µ) in some corner of the display. These metric prefix telltales are easy to overlook when reading the display of a digital meter, so pay close attention!
The measured value of current should agree closely with your Ohm’s Law calculation. Now, take that calculated value for current and multiply it by the respective resistances of each resistor to predict their voltage drops (E=IR). Switch you multimeter to the “voltage” mode and measure the voltage dropped across each resistor, verifying the accuracy of your predictions. Again, there should be close agreement between the calculated and measured voltage figures.
Each resistor voltage drop will be some fraction or percentage of the total voltage, hence the name voltage divider given to this circuit. This fractional value is determined by the resistance of the particular resistor and the total resistance. If a resistor drops 50% of the total battery voltage in a voltage divider circuit, that proportion of 50% will remain the same as long as the resistor values are not altered. So, if the total voltage is 6 volts, the voltage across that resistor will be 50% of 6, or 3 volts. If the total voltage is 20 volts, that resistor will drop 10 volts, or 50% of 20 volts.
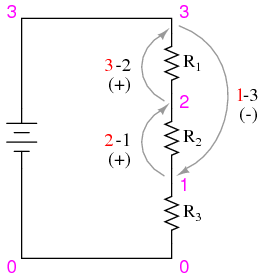
The next part of this experiment is a validation of Kirchhoff’s Voltage Law. For this, you need to identify each unique point in the circuit with a number. Points that are electrically common (directly connected to each other with insignificant resistance between) must bear the same number. An example using the numbers 0 through 3 is shown here in both illustrative and schematic form. In the illustration, I show how points in the circuit may be labeled with small pieces of tape, numbers written on the tape:
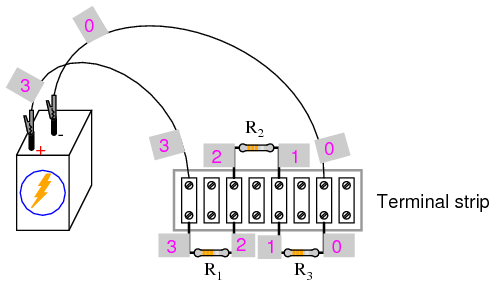
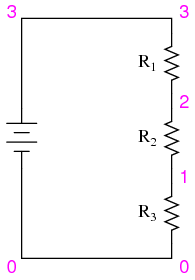
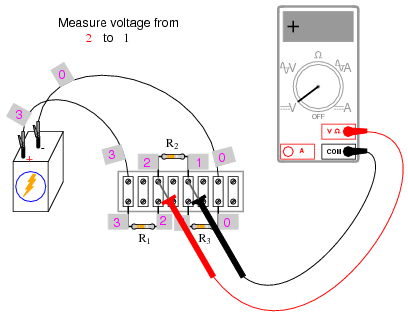
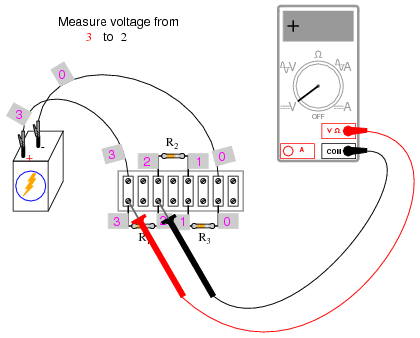
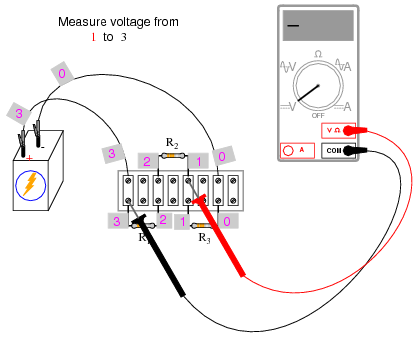
Using a digital voltmeter (this is important!), measure voltage drops around the loop formed by the points 0-1-2-3-0. Write on paper each of these voltages, along with its respective sign as indicated by the meter. In other words, if the voltmeter registers a negative voltage such as -1.325 volts, you should write that figure as a negative number. Do not reverse the meter probe connections with the circuit to make the number read “correctly.” Mathematical sign is very significant in this phase of the experiment! Here is a sequence of illustrations showing how to “step around” the circuit loop, starting and ending at point 0:
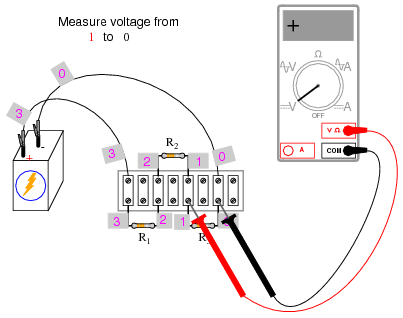
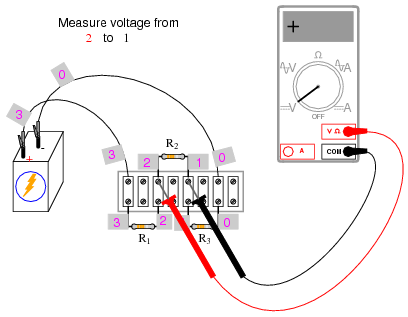
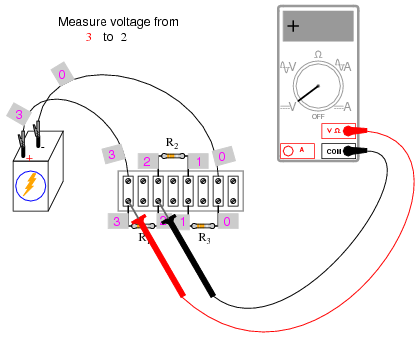
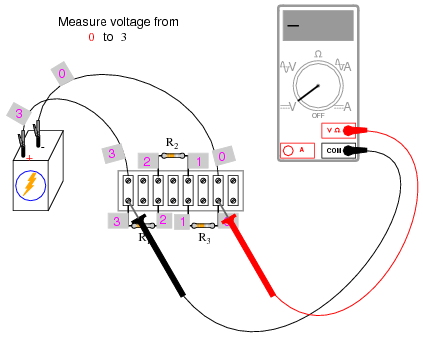
Using the voltmeter to “step” around the circuit in this manner yields three positive voltage figures and one negative:
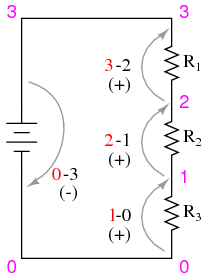
These figures, algebraically added (“algebraically” = respecting the signs of the numbers), should equal zero. This is the fundamental principle of Kirchhoff’s Voltage Law: that the algebraic sum of all voltage drops in a “loop” add to zero.
It is important to realize that the “loop” stepped around does not have to be the same path that current takes in the circuit, or even a legitimate current path at all. The loop in which we tally voltage drops can be any collection of points, so long as it begins and ends with the same point. For example, we may measure and add the voltages in the loop 1-2-3-1, and they will form a sum of zero as well:
.png?revision=1)
.png?revision=1)
Try stepping between any set of points, in any order, around your circuit and see for yourself that the algebraic sum always equals zero. This Law holds true no matter what the configuration of the circuit: series, parallel, series-parallel, or even an irreducible network.
Kirchhoff’s Voltage Law is a powerful concept, allowing us to predict the magnitude and polarity of voltages in a circuit by developing mathematical equations for analysis based on the truth of all voltages in a loop adding up to zero. This experiment is intended to give empirical evidence for and a deep understanding of Kirchhoff’s Voltage Law as a general principle.
COMPUTER SIMULATION
Netlist (make a text file containing the following text, verbatim):This computer simulation is based on the point numbers shown in the previous diagrams for illustrating Kirchhoff’s Voltage Law (points 0 through 3). Resistor values were chosen to provide 50%, 30%, and 20% proportions of total voltage across R1, R2, and R3, respectively. Feel free to modify the voltage source value (in the “.dc” line, shown here as 6 volts), and/or the resistor values.
When run, SPICE will print a line of text containing four voltage figures, then another line of text containing three voltage figures, along with lots of other text lines describing the analysis process. Add the voltage figures in each line to see that the sum is zero.


