3.6: Potentiometer as a Voltage Divider
- Page ID
- 1255
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- Two 6-volt batteries
- Carbon pencil “lead” for a mechanical-style pencil
- Potentiometer, single turn, 5 kΩ to 50 kΩ, linear taper (Radio Shack catalog # 271-1714 through 271-1716)
- Potentiometer, multi turn, 1 kΩ to 20 kΩ, (Radio Shack catalog # 271-342, 271-343, 900-8583, or 900-8587 through 900-8590)
Potentiometers are variable voltage dividers with a shaft or slide control for setting the division ratio. They are manufactured in panel-mount as well as breadboard (printed-circuit board) mount versions. Any style of potentiometer will suffice for this experiment.
If you salvage a potentiometer from an old radio or other audio device, you will likely be getting what is called an audio taper potentiometer. These potentiometers exhibit a logarithmic relationship between division ratio and shaft position. By contrast, a linear potentiometer exhibits a direct correlation between shaft position and voltage division ratio. I highly recommend a linear potentiometer for this experiment, and for most experiments in general.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 1, chapter 6: “Divider Circuits and Kirchhoff’s Laws”
LEARNING OBJECTIVES
- Voltmeter use
- Ohmmeter use
- Voltage divider design and function
- How voltages add in series
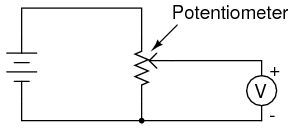
SCHEMATIC DIAGRAM
ILLUSTRATION
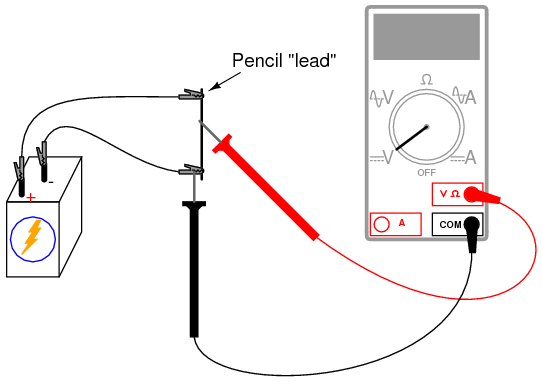
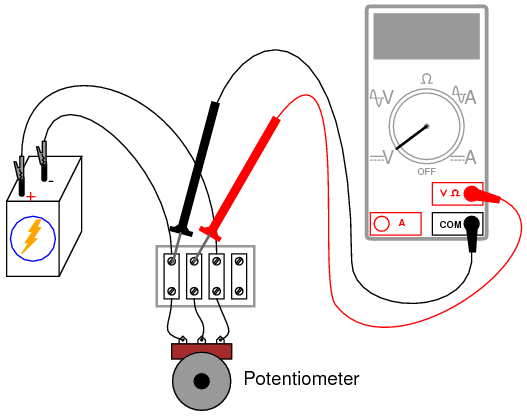
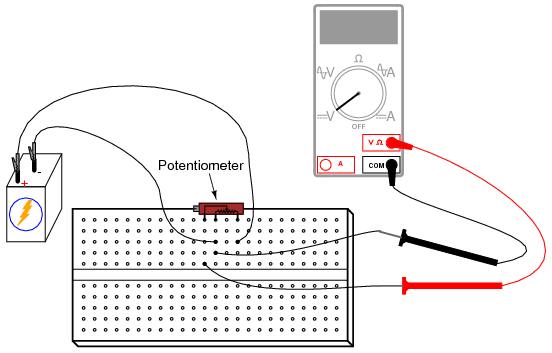
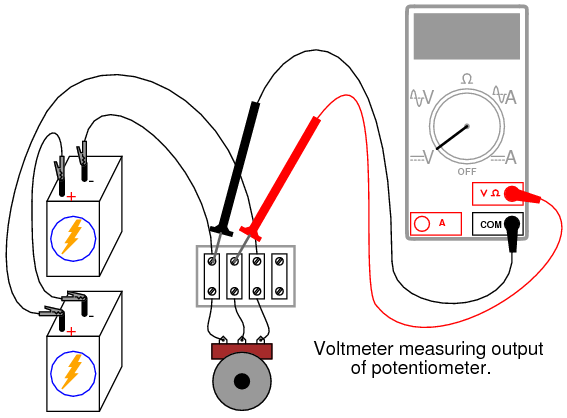
INSTRUCTIONS
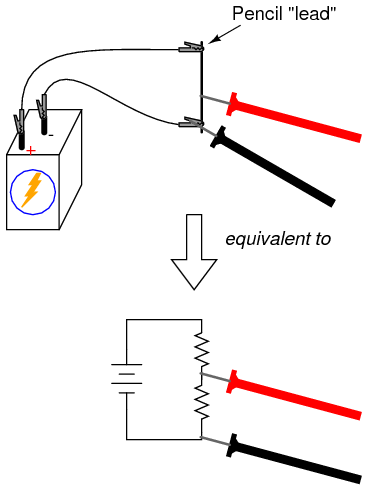
Begin this experiment with the pencil “lead” circuit. Pencils use a rod made of a graphite-clay mixture, not lead (the metal), to make black marks on paper. Graphite, being a mediocre electrical conductor, acts as a resistor connected across the battery by the two alligator-clip jumper wires. Connect the voltmeter as shown and touch the red test probe to the graphite rod. Move the red probe along the length of the rod and notice the voltmeter’s indication change. What probe position gives the greatest voltage indication?
Essentially, the rod acts as a pair of resistors, the ratio between the two resistances established by the position of the red test probe along the rod’s length:
Now, change the voltmeter connection to the circuit so as to measure voltage across the “upper resistor” of the pencil lead, like this:
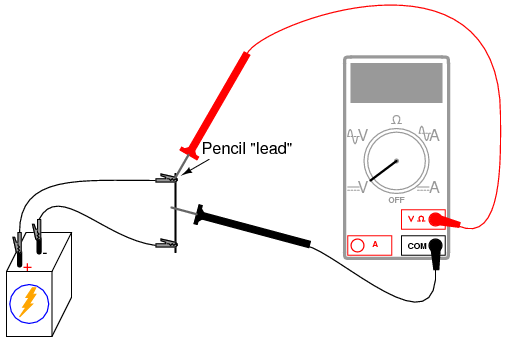
Move the black test probe position along the length of the rod, noting the voltmeter indication. Which position gives the greatest voltage drop for the meter to measure? Does this differ from the previous arrangement? Why?
Manufactured potentiometers enclose a resistive strip inside a metal or plastic housing, and provide some kind of mechanism for moving a “wiper” across the length of that resistive strip. Here is an illustration of a rotary potentiometer’s construction:
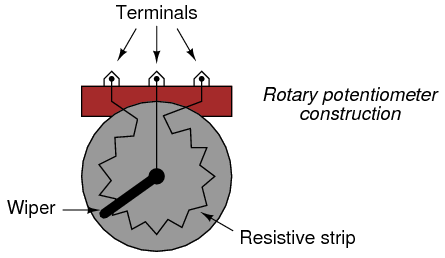
Some rotary potentiometers have a spiral resistive strip, and a wiper that moves axially as it rotates, so as to require multiple turns of the shaft to drive the wiper from one end of the potentiometer’s range to the other. Multi-turn potentiometers are used in applications where precise setting is important.
Linear potentiometers also contain a resistive strip, the only difference being the wiper’s direction of travel. Some linear potentiometers use a slide mechanism to move the wiper, while others a screw, to facilitate multiple-turn operation:
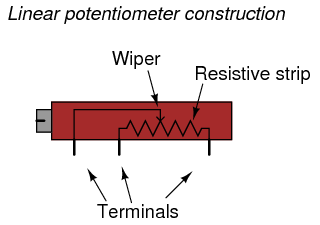
It should be noted that not all linear potentiometers have the same pin assignments. On some, the middle pin is the wiper.
Set up a circuit using a manufactured potentiometer, not the “home-made” one made from a pencil lead. You may use any form of construction that is convenient.
Measure battery voltage while powering the potentiometer, and make note of this voltage figure on paper. Measure voltage between the wiper and the potentiometer end connected to the negative (-) side of the battery. Adjust the potentiometer mechanism until the voltmeter registers exactly 1/3 of total voltage. For a 6-volt battery, this will be approximately 2 volts.
Now, connect two batteries in a series-aiding configuration, to provide approximately 12 volts across the potentiometer. Measure the total battery voltage, and then measure the voltage between the same two points on the potentiometer (wiper and negative side). Divide the potentiometer’s measured output voltage by the measured total voltage. The quotient should be 1/3, the same voltage division ratio as was set previously: