3.11: Make Your Own Multimeter
- Page ID
- 2143
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- Sensitive meter movement (Radio Shack catalog # 22-410)
- Selector switch, single-pole, multi-throw, break-before-make (Radio Shack catalog # 275-1386 is a 2-pole, 6-position unit that works well)
- Multi-turn potentiometers, PCB mount (Radio Shack catalog # 271-342 and 271-343 are 15-turn, 1 kΩ and 10 kΩ “trimmer” units, respectively)
- Assorted resistors, preferably high-precision metal film or wire-wound types (Radio Shack catalog # 271-309 is an assortment of metal-film resistors, +/- 1% tolerance)
- Plastic or metal mounting box
- Three “banana” jack style binding posts, or other terminal hardware, for connection to potentiometer circuit (Radio Shack catalog # 274-662 or equivalent)
The most important and expensive component in a meter is the movement: the actual needle-and-scale mechanism whose task it is to translate an electrical current into mechanical displacement where it may be visually interpreted. The ideal meter movement is physically large (for ease of viewing) and as sensitive as possible (requires minimal current to produce full-scale deflection of the needle). High-quality meter movements are expensive, but Radio Shack carries some of acceptable quality that are reasonably priced. The model recommended in the parts list is sold as a voltmeter with a 0-15 volt range, but is actually a milliammeter with a range (“multiplier”) resistor included separately.
It may be cheaper to purchase an inexpensive analog meter and disassemble it for the meter movement alone. Although the thought of destroying a working multimeter in order to have parts to make your own may sound counter-productive, the goal here is learning, not meter function.
I cannot specify resistor values for this experiment, as these depend on the particular meter movement and measurement ranges chosen. Be sure to use high-precision fixed-value resistors rather than carbon-composition resistors. Even if you happen to find carbon-composition resistors of just the right value(s), those values will change or “drift” over time due to aging and temperature fluctuations. Of course, if you don’t care about the long-term stability of this meter but are building it just for the learning experience, resistor precision matters little.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 1, chapter 8: “DC Metering Circuits”
LEARNING OBJECTIVES
- Voltmeter design and use
- Ammeter design and use
- Rheostat range limiting
- Calibration theory and practice
- Soldering practice
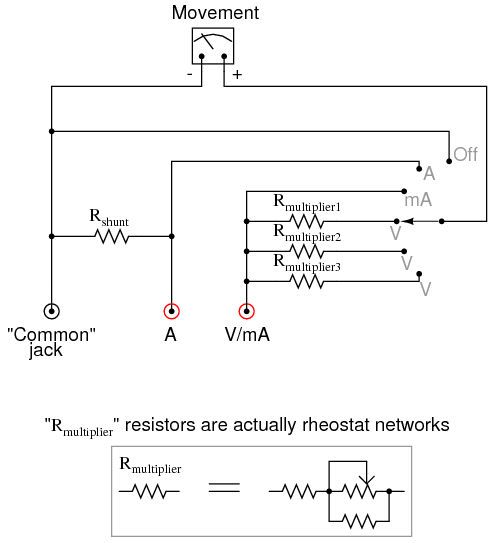
SCHEMATIC DIAGRAM
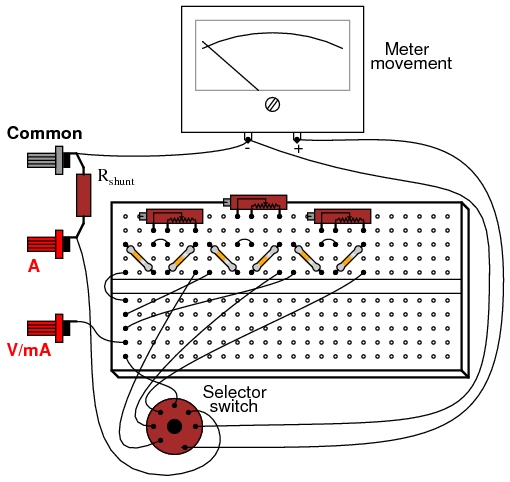
ILLUSTRATION
INSTRUCTIONS
First, you need to determine the characteristics of your meter movement. Most important is to know the full-scale deflection in milliamps or microamps. To determine this, connect the meter movement, a potentiometer, battery, and digital ammeter in series. Adjust the potentiometer until the meter movement is deflected exactly to full-scale. Read the ammeter’s display to find the full-scale current value:
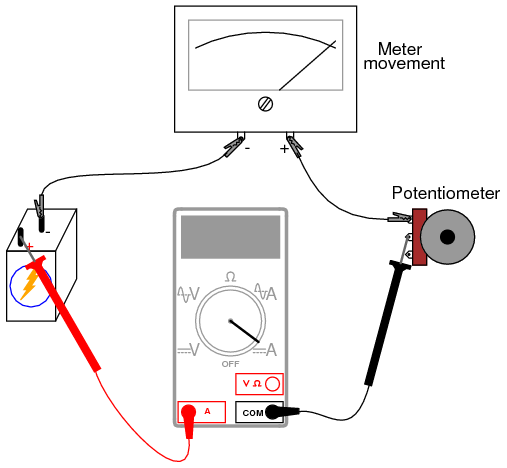
Be very careful not to apply too much current to the meter movement, as movements are very sensitive devices and easily damaged by overcurrent. Most meter movements have full-scale deflection current ratings of 1 mA or less, so choose a potentiometer value high enough to limit current appropriately, and begin testing with the potentiometer turned to maximum resistance. The lower the full-scale current rating of a movement, the more sensitive it is.
After determining the full-scale current rating of your meter movement, you must accurately measure its internal resistance. To do this, disconnect all components from the previous testing circuit and connect your digital ohmmeter across the meter movement terminals. Record this resistance figure along with the full-scale current figure obtained in the last procedure.
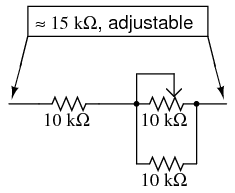
Perhaps the most challenging portion of this project is determining the proper range resistance values and implementing those values in the form of rheostat networks. The calculations are outlined in chapter 8 of volume 1 (“Metering Circuits”), but an example is given here. Suppose your meter movement had a full-scale rating of 1 mA and an internal resistance of 400 Ω. If we wanted to determine the necessary range resistance (“Rmultiplier”) to give this movement a range of 0 to 15 volts, we would have to divide 15 volts (total applied voltage) by 1 mA (full-scale current) to obtain the total probe-to-probe resistance of the voltmeter (R=E/I). For this example, that total resistance is 15 kΩ. From this total resistance figure, we subtract the movement’s internal resistance, leaving 14.6 kΩ for the range resistor value. A simple rheostat network to produce 14.6 kΩ (adjustable) would be a 10 kΩ potentiometer in parallel with a 10 kΩ fixed resistor, all in series with another 10 kΩ fixed resistor:
One position of the selector switch directly connects the meter movement between the black Common binding post and the red V/mA binding post. In this position, the meter is a sensitive ammeter with a range equal to the full-scale current rating of the meter movement. The far clockwise position of the switch disconnects the positive (+) terminal of the movement from either red binding post and shorts it directly to the negative (-) terminal. This protects the meter from electrical damage by isolating it from the red test probe, and it “dampens” the needle mechanism to further guard against mechanical shock.
The shunt resistor (Rshunt) necessary for a high-current ammeter function needs to be a low-resistance unit with a high power dissipation. You will definitely not be using any 1/4 watt resistors for this unless you form a resistance network with several smaller resistors in parallel combination. If you plan on having an ammeter range in excess of 1 amp, I recommend using a thick piece of wire or even a skinny piece of sheet metal as the “resistor,” suitably filed or notched to provide just the right amount of resistance.
To calibrate a home-made shunt resistor, you will need to connect the your multimeter assembly to a calibrated source of high current, or a high-current source in series with a digital ammeter for reference. Use a small metal file to shave off shunt wire thickness or to notch the sheet metal strip in small, careful amounts. The resistance of your shunt will increase with every stroke of the file, causing the meter movement to deflect more strongly. Remember that you can always approach the exact value in slower and slower steps (file strokes), but you cannot go “backward” and decrease the shunt resistance!
Build the multimeter circuit on a breadboard first while determining proper range resistance values, and perform all calibration adjustments there. For final construction, solder the components onto a printed circuit board. Radio Shack sells printed circuit boards that have the same layout as a breadboard, for convenience (catalog # 276-170). Feel free to alter the component layout from what is shown.
I strongly recommend that you mount the circuit board and all components in a sturdy box so that the meter is durably finished. Despite the limitations of this multimeter (no resistance function, inability to measure alternating current, and lower precision than most purchased analog multimeters), it is an excellent project to assist learning fundamental instrument principles and circuit function. A far more accurate and versatile multimeter may be constructed using many of the same parts if an amplifier circuit is added to it, so save the parts and pieces for a later experiment!


