5.15: JFET Current Regulator
- Page ID
- 2184
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- One N-channel junction field-effect transistor, models 2N3819 or J309 recommended (Radio Shack catalog # 276-2035 is the model 2N3819)
- Two 6-volt batteries
- One 10 kΩ potentiometer, single-turn, linear taper (Radio Shack catalog # 271-1715)
- One 1 kΩ resistor
- One 10 kΩ resistor
- Three 1.5 kΩ resistors
For this experiment you will need an N-channel JFET, not a P-channel!experiment you will need an N-channel JFET, not a P-channel!
Beware that not all transistors share the same terminal designations, or pinouts, even if they share the same physical appearance. This will dictate how you connect the transistors together and to other components, so be sure to check the manufacturer’s specifications (component datasheet), easily obtained from the manufacturer’s website. Beware that it is possible for the transistor’s package and even the manufacturer’s datasheet to show incorrect terminal identification diagrams! Double-checking pin identities with your multimeter’s “diode check” function is highly recommended. For details on how to identify junction field-effect transistor terminals using a multimeter, consult chapter 5 of the Semiconductor volume (volume III) of this book series.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 3, chapter 5: “Junction Field-Effect Transistors”
Lessons In Electric Circuits, Volume 3, chapter 3: “Diodes and Rectifiers”
LEARNING OBJECTIVES
- How to use a JFET as a current regulator
- How the JFET is relatively immune to changes in temperature
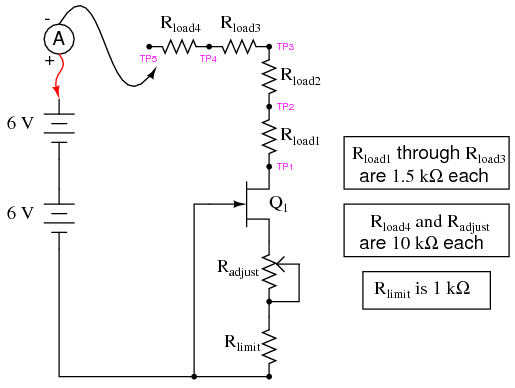
SCHEMATIC DIAGRAM
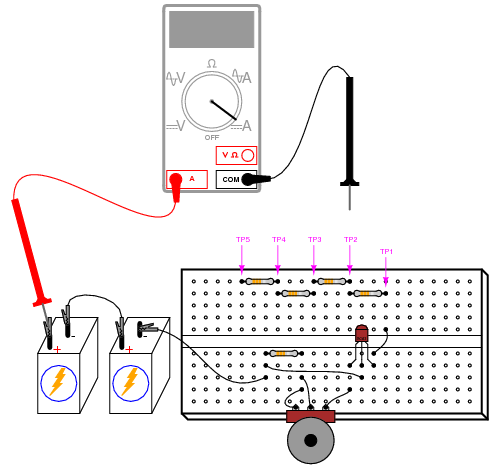
ILLUSTRATION
INSTRUCTIONS
Previously in this chapter, you saw how a pair of bipolar junction transistors (BJTs) could be used to form a current mirror, whereby one transistor would try to maintain the same current through it as though the other, the other’s current level is established by a variable resistance. This circuit performs the same task of regulating current but uses a single junction field-effect transistor (JFET) instead of two BJTs.
The two series resistors Radjust and Rlimit set the current regulation point, while the load resistors and the test points between them serve only to demonstrate constant current despite changes in load resistance.
To begin the experiment, touch the test probe to TP4 and adjust the potentiometer through its range of travel. You should see a small, changing current indicated by your ammeter as you move the potentiometer mechanism: no more than a few milliamps. Leave the potentiometer set to a position giving a round number of milliamps and move the meter’s black test probe to TP3. The current indication should be very nearly the same as before. Move the probe to TP2, then TP1. Again, you should see a nearly unchanged amount of current. Try adjusting the potentiometer to another position, giving a different current indication, and touch the meter’s black probe to test points TP1 through TP4, noting the stability of the current indications as you change load resistance. This demonstrates the current regulating behavior of this circuit.
TP5, at the end of a 10 kΩ resistor, is provided for introducing a large change in load resistance. Connecting the black test probe of your ammeter to that test point gives a combined load resistance of 14.5 kΩ, which will be too much resistance for the transistor to maintain the maximum regulated current through. To experience what I’m describing here, touch the black test probe to TP1 and adjust the potentiometer for maximum current. Now, move the black test probe to TP2, then TP3, then TP4. For all these test point positions, the current will remain approximately constant. However, when you touch the black probe to TP5, the current will fall dramatically. Why? Because at this level of load resistance, there is an insufficient voltage drop across the transistor to maintain regulation. In other words, the transistor will be saturated as it attempts to provide more current than the circuit resistance will allow.
Move the black test probe back to TP1 and adjust the potentiometer for minimum current. Now, touch the black test probe to TP2, then TP3, then TP4, and finally TP5. What do you notice about the current indication at all these points? When the current regulation point is adjusted to a lesser value, the transistor is able to maintain regulation over a much larger range of load resistance.
An important caveat with the BJT current mirror circuit is that both transistors must be at equal temperature for the two currents to be equal. With this circuit, however, transistor temperature is almost irrelevant. Try grasping the transistor between your fingers to heat it up, noting the load current with your ammeter. Try cooling it down afterward by blowing on it. Not only is the requirement of transistor matching eliminated (due to the use of just one transistor), but the thermal effects are all but eliminated as well due to the relative thermal immunity of the field-effect transistor. This behavior also makes field-effect transistors immune to thermal runaway; a decided advantage over bipolar junction transistors.
An interesting application of this current-regulator circuit is the so-called constant-current diode. Described in the “Diodes and Rectifiers” chapter of volume III, this diode isn’t really a PN junction device at all. Instead, it is a JFET with a fixed resistance connected between the gate and source terminals:
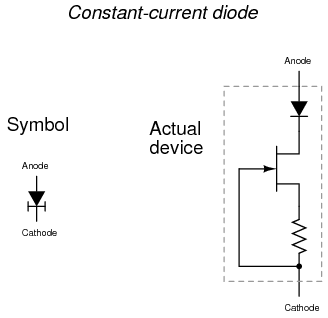
A normal PN-junction diode is included in series with the JFET to protect the transistor against damage from reverse-bias voltage, but otherwise the current-regulating facility of this device is entirely provided by the field-effect transistor.
COMPUTER SIMULATION
Schematic with SPICE node numbers:
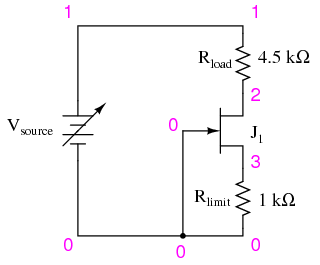
SPICE does not allow for “sweeping” resistance values, so to demonstrate the current regulation of this circuit over a wide range of conditions, I’ve elected to sweep the source voltage from 6 to 12 volts in 0.1-volt steps. If you wish, you can set rload to different resistance values and verify that the circuit current remains constant. With an rlimit value of 1 kΩ, the regulated current will be 291.8 µA. This current figure will most likely not be the same as your actual circuit current, due to differences in JFET parameters.
Many manufacturers give SPICE model parameters for their transistors, which may be typed in the .modelline of the netlist for a more accurate circuit simulation.


