7.2: Basic Gate Function
- Page ID
- 1279
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Parts and Materials
- 4011 quad NAND gate (Radio Shack catalog # 276-2411)
- Eight-position DIP switch (Radio Shack catalog # 275-1301)
- Ten-segment bar graph LED (Radio Shack catalog # 276-081)
- One 6 volt battery
- Two 10 kΩ resistors
- Three 470 Ω resistors
Caution! The 4011 IC is CMOS, and therefore sensitive to static electricity!
Further Reading
Lessons In Electric Circuits, Volume 4, chapter 3: “Logic Gates”
Learning Objectives
- Purpose of a “pulldown” resistor
- How to experimentally determine the truth table of a gate
- How to connect logic gates together
- How to create different logical functions by using NAND gates
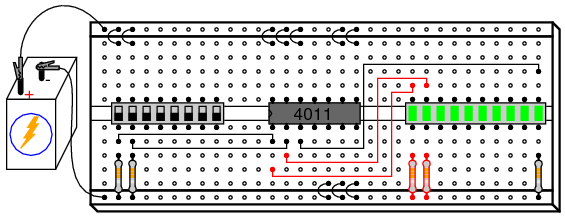
Basic Gate Function Schematic Diagram
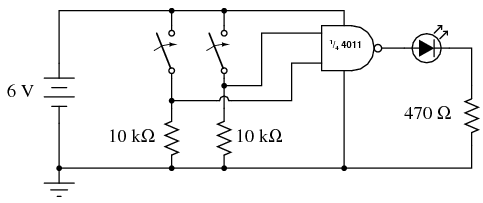
Basic Gate Function Illustration
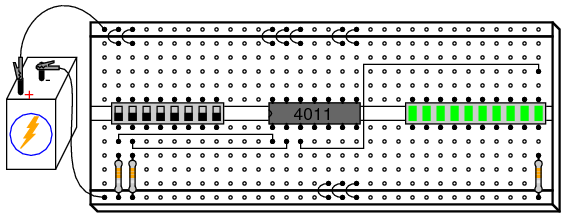
Experiment Instructions
To begin, connect a single NAND gate to two input switches and one LED, as shown. At first, the use of an 8-position switch and a 10-segment LED bar graph may seem excessive since only two switches and one LED are needed to show the operation of a single NAND gate. However, the presence of those extra switches and LEDs make it very convenient to expand the circuit and help make the circuit layout both clean and compact.
It is highly recommended that you have a datasheet for the 4011 chip available when you build your circuit. Don’t just follow the illustration shown above! It is important that you develop the skill of reading datasheets, especially “pinout” diagrams when connecting IC terminals to other circuit elements. The datasheet’s connection diagram is an essential piece of information to have. Shown here is my own rendition of what any 4011 datasheet shows:
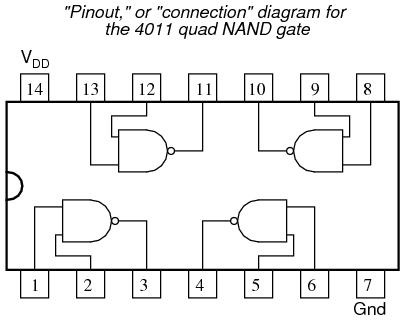
In the breadboard illustration, I’ve shown the circuit built using the lower-left NAND gate: pin #‘s 1 and 2 are the inputs, and pin #3 is the output. Pin #‘s 14 and 7 conduct DC power to all four gate circuits inside the IC chip, “VDD” representing the positive side of the power supply (+V), and “Gnd” representing the negative side of the power supply (-V), or ground. Sometimes the negative power supply terminal will be labeled “VSS” instead of “Gnd” on a datasheet, but it means the same thing.
Digital logic circuitry does not make use of split power supplies as op-amps do. Like op-amp circuits, though, ground is still the implicit point of reference for all voltage measurements. If I were to speak of a “high” signal being present on a certain pin of the chip, I would mean that there was full voltage between that pin and the negative side of the power supply (ground).
Note how all inputs of the unused gates inside the 4011 chip are connected either to VDD or ground. This is not a mistake, but an act of intentional design. Since the 4011 is a CMOS integrated circuit, and CMOS circuit inputs left unconnected (floating) can assume any voltage level merely from intercepting a static electric charge from a nearby object, leaving inputs floating means that those unused gates may receive any random combinations of “high” and “low” signals.
Why is this undesirable, if we aren’t using those gates? Who cares what signals they receive, if we are not doing anything with their outputs? The problem is if static voltage signals appear at the gate inputs that are not fully “high” or fully “low,” the gates’ internal transistors may begin to turn on in such a way as to draw excessive current. At worst, this could lead to damage of the chip. At best it means excessive power consumption. It matters little if we choose to connect these unused gate inputs “high” (VDD) or “low” (ground), so long as we connect them to one of those two places. In the breadboard illustration, I show all the top inputs connected to VDD, and all the bottom inputs (of the unused gates) connected to ground. This was done merely because those power supply rail holes were closer and did not require long jumper wires!
Please note that none of the unused gate outputs have been connected to VDD or ground, and for good reason! If I were to do that, I may be forcing a gate to assume the opposite output state that it’s trying to achieve, which is a complicated way of saying that I would have created a short-circuit. Imagine a gate that is supposed to output a “high” logic level (for a NAND gate, this would be true if any of its inputs were “low”). If such a gate were to have its output terminal directly connected to ground, it could never reach a “high” state (being made electrically common to ground through the jumper wire connection). Instead, its upper (P-channel) output transistor would be turned on in vain, sourcing maximum current to a nonexistent load. This would very likely damage the gate! Gate output terminals, by their very nature, generate their own logic levels and never “float” in the same way that CMOS gate inputs do.
The two 10 kΩ resistors are placed in the circuit to avoid floating input conditions on the used gate. With a switch closed, the respective input will be directly connected to VDD and therefore be “high.” With a switch open, the 10 kΩ “pulldown” resistor provides a resistive connection to ground, ensuring a secure “low” state at the gate’s input terminal. This way, the input will not be susceptible to stray static voltages.
With the NAND gate connected to the two switches and one LED as shown, you are ready to develop a “truth table” for the NAND gate. Even if you already know what a NAND gate truth table looks like, this is a good exercise in experimentation: discovering a circuit’s behavioral principles by induction. Draw a truth table on a piece of paper like this:
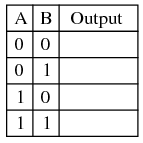
The “A” and “B” columns represent the two input switches, respectively. When the switch is on, its state is “high” or 1. When the switch is off, its state is “low,” or 0, as ensured by its pulldown resistor. The gate’s output, of course, is represented by the LED: whether it is lit (1) or unlit (0). After placing the switches in every possible combination of states and recording the LED’s status, compare the resulting truth table with what a NAND gate’s truth table should be.
As you can imagine, this breadboard circuit is not limited to testing NAND gates. Any gate type may be tested with two switches, two pulldown resistors, and an LED to indicate output status. Just be sure to double-check the chip’s “pinout” diagram before substituting it pin-for-pin in place of the 4011. Not all “quad” gate chips have the same pin assignments!
Additional Improvement
An improvement you might want to make to this circuit is to assign a couple of LEDs to indicate input status, in addition to the one LED assigned to indicate the output. This makes operation a little more interesting to observe, and has the further benefit of indicating if a switch fails to close (or open) by showing the true input signal to the gate, rather than forcing you to infer input status from switch position: