7.3: NOR Gate S-R Latch
- Page ID
- 1280
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- 4001 quad NOR gate (Radio Shack catalog # 276-2401)
- Eight-position DIP switch (Radio Shack catalog # 275-1301)
- Ten-segment bar graph LED (Radio Shack catalog # 276-081)
- One 6 volt battery
- Two 10 kΩ resistors
- Two 470 Ω resistors
- Two 100 Ω resistors
Caution! The 4001 IC is CMOS, and therefore sensitive to static electricity!
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 4, chapter 3: “Logic Gates”
Lessons In Electric Circuits, Volume 4, chapter 10: “Multivibrators”
LEARNING OBJECTIVES
- The effects of positive feedback in a digital circuit
- What is meant by the “invalid” state of a latch circuit
- What a race condition is in a digital circuit
- The importance of valid “high” CMOS signal voltage levels
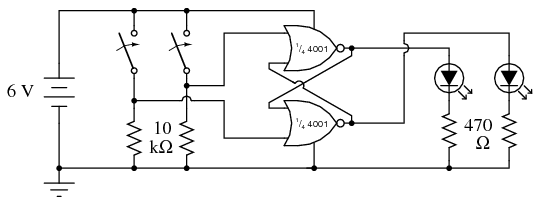
SCHEMATIC DIAGRAM
ILLUSTRATION
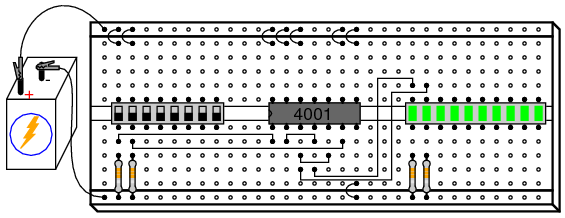
INSTRUCTIONS
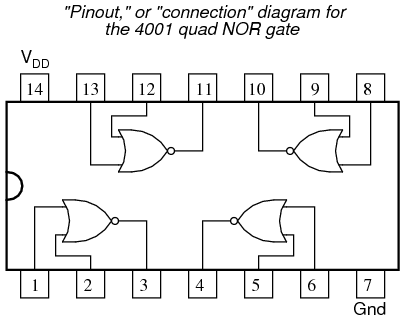
The 4001 integrated circuit is a CMOS quad NOR gate, identical in input, output, and power supply pin assignments to the 4011 quad NAND gate. Its “pinout,” or “connection,” diagram is as such:
When two NOR gates are cross-connected as shown in the schematic diagram, there will be positive feedback from output to input. That is, the output signal tends to maintain the gate in its last output state. Just as in op-amp circuits, positive feedback creates hysteresis. This tendency for the circuit to remain in its last output state gives it a sort of “memory.” In fact, there are solid-state computer memory technologies based on circuitry like this!
If we designate the left switch as the “Set” input and the right switch as the “Reset,” the left LED will be the “Q” output and the right LED the “Q-not” output. With the Set input “high” (switch on) and the Reset input “low,” Q will go “high” and Q-not will go “low.” This is known as the set state of the circuit. Making the Reset input “high” and the Set input “low” reverses the latch circuit’s output state: Q “low” and Q-not “high.” This is known as the reset state of the circuit. If both inputs are placed into the “low” state, the circuit’s Q and Q-not outputs will remain in their last states, “remembering” their prior settings. This is known as the latched state of the circuit.
Because the outputs have been designated “Q” and “Q-not,” it is implied that their states will always be complementary (opposite). Thus, if something were to happen that forced both outputs to the same state, we would be inclined to call that mode of the circuit “invalid.” This is exactly what will happen if we make both Set and Reset inputs “high:” both Q and Q-not outputs will be forced to the same “low” logic state. This is known as the invalid or illegal state of the circuit, not because something has gone wrong, but because the outputs have failed to meet the expectations established by their labels.
Since the “latched” state is a hysteretic condition whereby the last output states are “remembered,” one might wonder what will happen if the circuit powers up this way, with no previous state to hold. To experiment, place both switches in their off positions, making both Set and Reset inputs low, then disconnect one of the battery wires from the breadboard. Then, quickly make and break contact between that battery wire and its proper connection point on the breadboard, noting the status of the two LEDs as the circuit is powered up again and again:
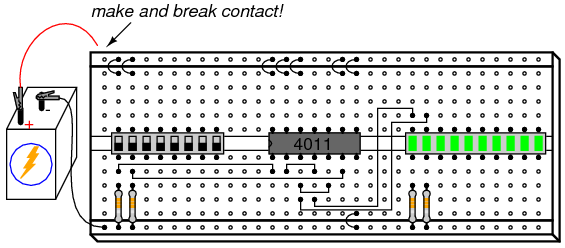
When a latch circuit such as this is powered up into its “latched” state, the gates race against each other for control. Given the “low” inputs, both gates try to output “high” signals. If one of the gates reaches its “high” output state before the other, that “high” state will be fed back to the other gate’s input to force its output “low,” and the race is won by the faster gate.
Invariably, one gate wins the race, due to internal variations between gates in the chip, and/or external resistances and capacitances that act to delay one gate more than the other. What this usually means is that the circuit tends to power up in the same mode, over and over again. However, if you are persistent in your powering/un-powering cycles, you should see at least a few times where the latch circuit powers up latched in the opposite state from normal.
Race conditions are generally undesirable in any kind of system, as they lead to unpredictable operation. They can be particularly troublesome to locate, as this experiment shows, because of the unpredictability they create. Imagine a scenario, for instance, where one of the two NOR gates was exceptionally slow-acting, due to a defect in the chip. This handicap would cause the other gate to win the power-up race every time. In other words, the circuit will be very predictable on power-up with both inputs “low.” However, suppose that the unusual chip was to be replaced by one with more evenly matched gates, or by a chip where the other NOR gate were consistently slower. Normal circuit behavior is not supposed to change when a component is replaced, but if race conditions are present, a change of components may very well do just that.
Due to the inherent race tendency of an S-R latch, one should not design a circuit with the expectation of a consistent power-up state, but rather use external means to “force” the race so that the desired gate always “wins.”
An interesting modification to try in this circuit is to replace one of the 470 Ω LED “dropping” resistors with a lower-value unit, such as 100 Ω. The obvious effect of this alteration will be increased LED brightness, as more current is allowed through. A not-so-obvious effect will also result, and it is this effect which holds great learning value. Try replacing one of the 470 Ω resistors with a 100 Ω resistor, and operate the input signal switches through all four possible setting combinations, noting the behavior of the circuit.
You should note that the circuit refuses to latch in one of its states (either Set or Reset), but only in the other state, when the input switches are both set “low” (the “latch” mode). Why is this? Take a voltmeter and measure the output voltage of the gate whose output is “high” when both inputs are “low.” Note this voltage indication, then set the input switches in such a way that the other state (either Reset or Set) is forced, and measure the output voltage of the other gate when its output is “high.” Note the difference between the two gate output voltage levels, one gate loaded by an LED with a 470 Ω resistor, and the other loaded by an LED with a 100 Ω resistor. The one loaded down by the “heavier” load (100 Ω resistor) will be much less: so much less than this voltage will not be interpreted by the other NOR gate’s input as a “high” signal at all as it is fed back! All logic gates have permissible “high” and “low” input signal voltage ranges, and if the voltage of a digital signal falls outside this permissible range, it might not be properly interpreted by the receiving gate. In a latch circuit such as this, which depends on a solid “high” signal fed back from the output of one gate to the input of the other, a “weak” signal will not be able to maintain the positive feedback necessary to keep the circuit latched in one of its states.
This is one reason I favor the use of a voltmeter as a logic “probe” for determining digital signal levels, rather than an actual logic probe with “high” and “low” lights. A logic probe may not indicate the presence of a “weak” signal, whereas a voltmeter definitely will by means of its quantitative indication. This type of problem, common in circuits where different “families” of integrated circuits are mixed (TTL and CMOS, for example), can only be found with test equipment providing quantitative measurements of signal level.


