3.1: Magnetic Fields
- Page ID
- 3272
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)If a magnet is suspended in the air, it will always turn and align with Earth's north and south poles. The two ends, called the magnetic poles, are where the force is strongest.
A magnetic field of force is set up between the two poles. You can think of it as invisible lines of force traveling from one pole to the other. The magnetic lines (flux lines) are continuous and always form loops. These invisible lines can be seen if you sprinkle iron filings on a piece of paper placed over a bar magnet (Figure \(\PageIndex{1}\)).
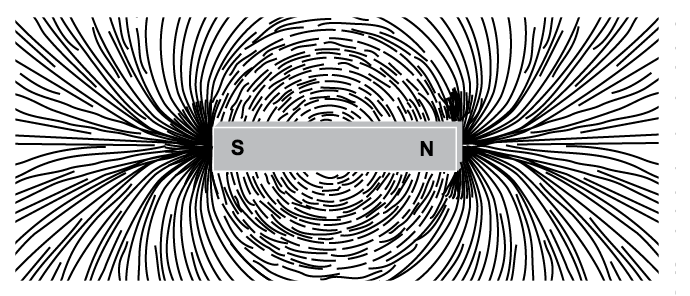
Characteristics of magnetic lines of force
Magnets have some specific rules governing their operation.
Magnetic lines of force possess direction
These lines are continuous and extend from the north pole to the south pole of the magnet (Figure \(\PageIndex{2}\)).
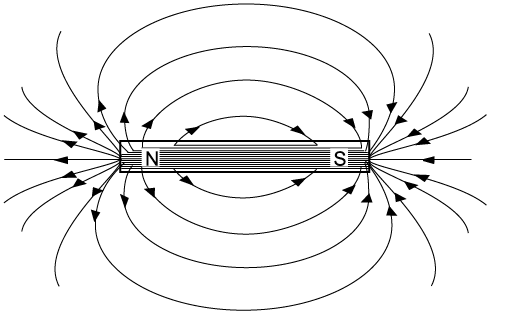
Magnetic lines of force always form complete loops
The lines do not begin and end at the poles but rather pass through the magnet to form complete loops. If you were to cut a magnet in half, you could observe the magnetic field between the two pieces of the magnet (Figure \(\PageIndex{3}\)).
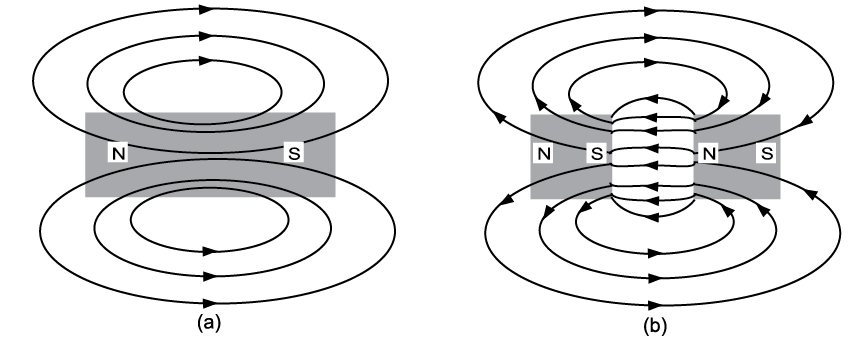
Magnetic lines of force always form tight loops
This rule explains the idea of attraction. The flux lines attempt to pull in as close to the magnet as possible, just like rubber bands. They also try to concentrate at each pole. If you place two unlike poles together, they try to become one big magnet and shorten the lines of force (Figure \(\PageIndex{4}\)).
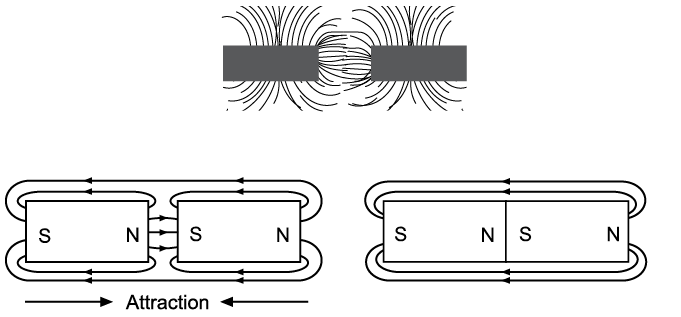
Magnetic lines of force repel each other
If magnetic lines of force act like rubber bands, why don’t they collapse into the center? The reason is that they repel each other. Look back at Figure 3; notice that the lines tend to diverge as they move away from the poles, rather than converge or even remain parallel. This results from their mutual repulsion.
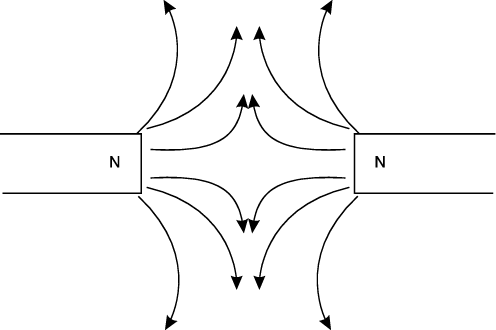
Magnetic lines of force never cross, but must always form individual loops
The mutual repulsion of each magnetic line accounts for this effect. This explains why like poles repel each other. If the lines cannot cross each other, then they must exert a force against each other. If you could see the lines of force, they would look like the diagram in (Figure \(\PageIndex{5}\)).
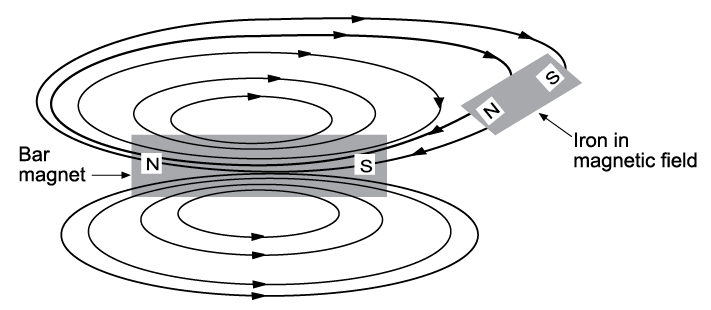
Magnetic lines of force can pass more easily through material that can be magnetized
The magnetic lines of force will distort to include a piece of iron in the field. This will have the effect of turning the iron into a temporary magnet. Then the opposite poles of the two magnets will attract each other and try to shorten the flux lines. This accounts for the attraction of unmagnetized ferromagnetic objects (Figure \(\PageIndex{6}\)).
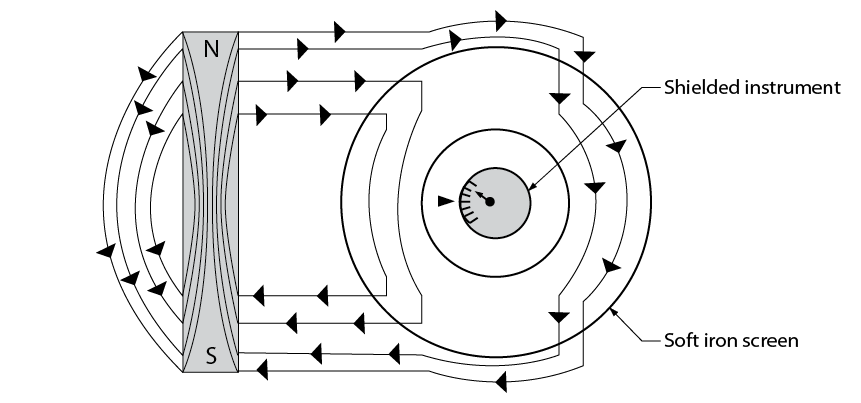
There is no insulation against magnetic lines of force
All magnetic field lines must terminate on the opposite pole, which means there is no way to stop them. Nature must find a way to return the magnetic field lines back to an opposite pole. However, magnetic fields can be rerouted around objects. This is a form of magnetic shielding. By surrounding an object with a material that can “conduct” magnetic flux better than the materials around it, the magnetic field will tend to flow along this material and avoid the objects inside. This allows the field lines to terminate on the opposite poles, but just gives them a different route to follow (Figure \(\PageIndex{7}\)).
Alignment of the atoms
If you took a permanent magnet and cut it in half, you would have two permanent magnets, each with a north and south pole. If you continued cutting each in half, you would have more magnets. This suggests that if you could cut right down to the atom, it would also be a perfect permanent magnet.
This theory can be extended to non-magnetic material as well. Each of the atoms is a magnet, but they are all pointing in different directions. If you can get enough atoms pointing in the same direction, you will have a magnet. All you have to do is expose the piece of metal to flux lines, and the atoms will align.
These atoms tend to form in groups called domains. When the domain becomes large enough, the entire piece of metal becomes the domain and exerts force. When all of the atoms become aligned, the piece has become saturated and cannot get any stronger.


