8.2: Unit 2: CNC Machine Tool Programmable Axes and Position Dimensioning Systems
- Page ID
- 2286
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)OBJECTIVE
After completing this unit, you should be able to:
- Understand the cartesian coordinate system.
- Understand the Cartesian coordinates of the plane.
- Understand the Cartesian coordinates of three-dimensional space.
- Understand the four Quadrants.
- Explain the difference between polar and rectangular coordinated.
- Identify the programmable axes on a CNC machining.
THE CARTESIAN COORDINATE SYSTEM
Cartesian coordinates allow one to specify the location of a point in the plane, or in three-dimensional space. The Cartesian coordinates or rectangular coordinates system of a point are a pair of numbers (in two-dimensions) or a triplet of numbers (in three-dimensions) that specified signed distances from the coordinate axis. First we must understand a coordinate system to define our directions and relative position. A system used to define points in space by establishing directions(axis) and a reference position(origin). A coordinate system can be rectangular or polar.
Just as points on the line can be placed in one to one correspondence with the real number line, so points in plane can be placed in one to one correspondence with pairs of real number line by using two coordinate lines. To do this, we construct two perpendicular coordinate line that intersect at their origins; for convenience. Assign a set of equally space graduations to the x and y axes starting at the origin and going in both directions, left and right (x axis) and up and down (y axis) point along each axis may be established. We make one of the number lines vertical with its positive direction upward and negative direction downward. The other number lines horizontal with its positive direction to the right and negative direction to the left. The two number lines are called coordinate axes; the horizontal line is the x axis, the vertical line is the y axis, and the coordinate axes together form the Cartesian coordinate system or a rectangular coordinate system. The point of intersection of the coordinate axes is denoted by O and is the origin of the coordinate system. See Figure 1.
Figure 1
It is basically, Two Real Number Lines Put Together, one going left-right, and the other going up-down. The horizontal line is called x-axis and the vertical line is called y-axis.
The Origin
The point (0,0) is given the special name “The Origin”, and is sometimes given the letter “O”.
Real Number Line
The basis of this system is the real number line marked at equal intervals. The axis is labeled (X, Y or Z). One point on the line is designated as the Origin. Numbers on one side of the line are marked as positive and those to the other side marked negative. See Figure 2.
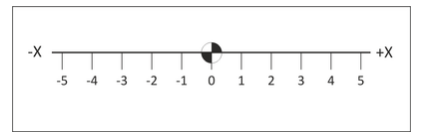
Figure 2. X-axis number line
Cartesian coordinates of the plane
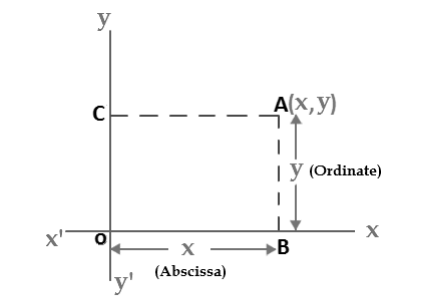
A plane in which a rectangular coordinate system has been introduced is a coordinate plane or an x-y-plane. We will now show how to establish a one to one correspondence between points in a coordinate plane and pairs of real number. If A is a point in a coordinate plane, then we draw two lines through A, one perpendicular to the x-axis and one perpendicular to the y-axis. If the first line intersects the x-axis at the point with coordinate x and the second line intersects the y-axis at the point with coordinate y, then we associate the pair (x,y) with the A( See Figure 2). The number a is the x-coordinate or abscissa of P and the number b is the y-coordinate or ordinate of p; we say that A is the point with coordinate (x,y) and denote the point by A(x,y). The point (0,0) is given the special name “The Origin”, and is sometimes given the letter “O”.
Abscissa and Ordinate:
The words “Abscissa” and “Ordinate” … they are just the x and y values:
- Abscissa: the horizontal (“x”) value in a pair of coordinates: how far along the point is.
- Ordinate: the vertical (“y”) value in a pair of coordinates: how far up or down the point is.