4.7: Lab Colour Space and Delta E Measurements
- Page ID
- 9525
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The CIE (Commission Internationale d’Eclairage or International Commission on Light) is a scientific body formed by colour scientists in the 1930s that has provided much of the fundamental colour knowledge we possess today. Three core definitions provided by the CIE are the standard observer, the Lab colour space, and Delta E measurements. The latter two are particularly important for colour management.
The Lab Colour Space Revisited
In section, 4.2, we mentioned the Lab colour space as a natural outgrowth of understanding the function of opponency in human vision. It’s comprised of three axes: L represents darkness to lightness, with values ranging from 0 to 100; a represents greenness to redness with values of -128 to +127; and b represents blueness to yellowness also with values from -128 to +127.
Notice that there are no negative values on the L axis as we can’t have less than zero light, which describes absolute darkness. The L axis is considered achromatic meaning without colour. Here we are dealing with the volume rather than the kind of light. In contrast, the a and b axes are chromatic, describing the colour character and the type of light.
The standard two-dimensional depiction is of only the a and b axes, with a as the horizontal axis and b as the vertical axis. This places red to the right, green to the left, blue at the bottom, and yellow at the top. If you found our previous mnemonic aid of POLO helpful, you can use RGBY to remember the colour pairs. For correct placement, remember that red is on the right, and blue is on the bottom.
Colours are more neutral and grey toward the centre of the colour space, along the L axis. Imagine that equivalent values of the opposing colours are cancelling each other out, reducing the saturation and intensity of those colours. The most saturated colours are at the extremes of the a and b axes, in both the large positive and negative numbers. For a visual depiction of the Lab colour space, open the ColorSync application found in the Utilities folder of any Macintosh computer and view one of the default profiles such as Adobe RGB.
Now it’s time to explore the practical application of this colour map for the comparative analysis of colour samples. We can’t make any progress in evaluating our success in colour matching unless we have a frame of reference, some yardstick to determine how much one colour sample is similar or different from another. That yardstick is the Delta E measurement.
Delta E
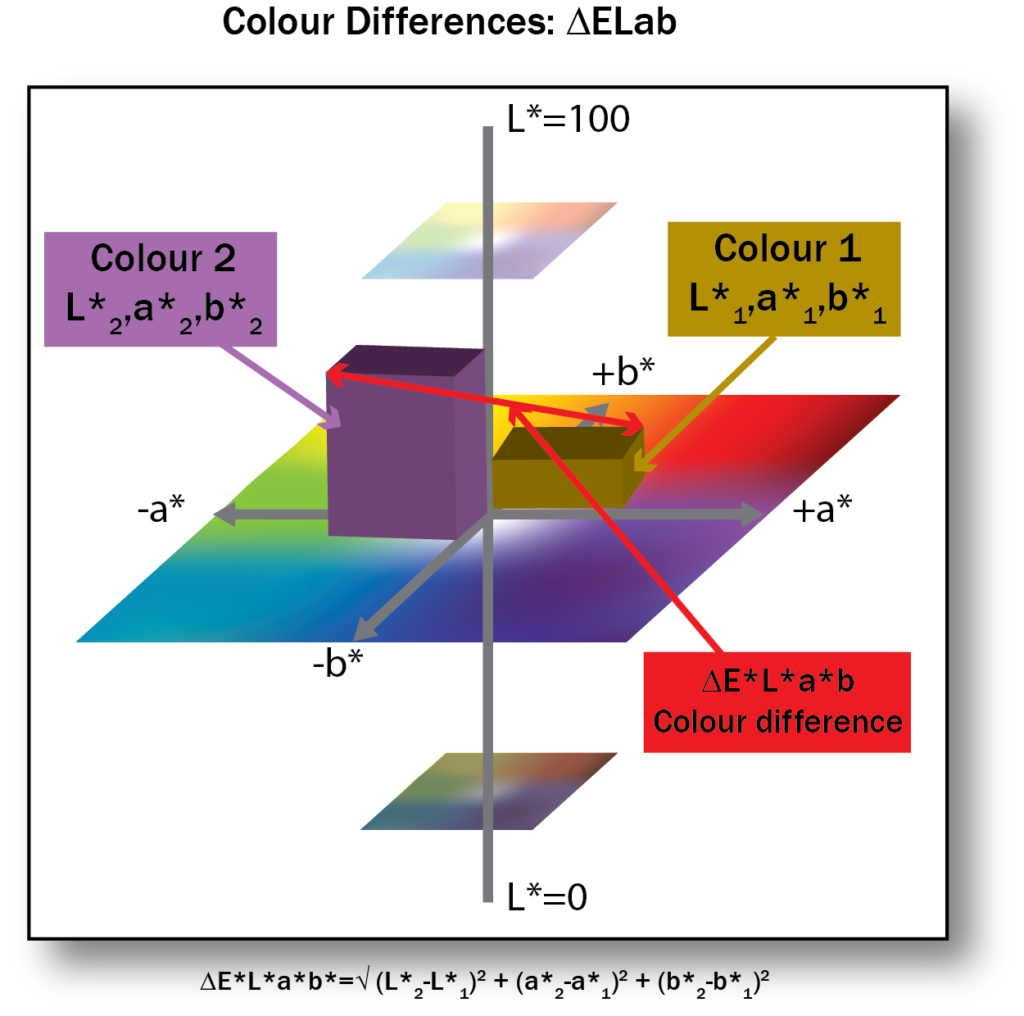
Delta, the fourth letter of the Greek alphabet and symbolized as a triangle, is used in science to indicate difference. Delta E is the difference between two colours designated as two points in the Lab colour space. With values assigned to each of the L, a, and b attributes of two colours, we can use simple geometry to calculate the distance between their two placements in the Lab colour space (see Figure 4.7).
How do we do that? It looks a lot like the formula used to determine the long side of a right triangle that you may remember from high school geometry. We square the difference between each of the L, a, and b values; add them all together; and take the square root of that sum. Written out as a formula it looks a little more daunting: ![]() .
.
Let’s try a simple example to see what we get. Colour 1 has a Lab value of 51, 2, 2 and Colour 2 is 50, 0, 0 (right at the centre of the colour space):
![]() , and
, and![]() , so our first value is 1.
, so our first value is 1.
![]() ; and
; and ![]() , so our second value is 4.
, so our second value is 4.
![]() , so the third value is also 4.
, so the third value is also 4.
Add them together: ![]() ; and take the square root:
; and take the square root: ![]() .
.
The Delta E (difference) between our two colours is 3. Could we detect that difference if we were viewing those two colours? Probably just barely. The minimum Delta E for seeing a difference is about 2. Smaller differences can normally be detected in neutral colours (such as our samples), while more saturated colours require a slightly larger Delta E. A Delta E of 4 is the upper threshold for acceptable machine repeatability or consistency.
Delta E provides a value indicating the overall difference between two colours. It does not provide any colour-related data such as which colour is lighter/darker, redder/greener, more blue/more yellow. To understand how the colours are different, we have to evaluate the comparative L, a, and b differences independently.
Experimentation over time has come to show that conventional Delta E is about 75% accurate in showing the difference we see between two colours. Delta E numbers exaggerate the differences in yellows and compress our perceptual distance between blues. To improve on the representation of our interpretation of colour difference, scientists have produced a modified formula known as Delta E(94).
Delta E(94)
Delta E(94) is a modified formula that provides about 95% accuracy in correlation to human perception of colour differences. Here it is in all its splendour:
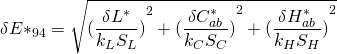
where:
![]()
![]()
![]()
![]() (for reference conditions)
(for reference conditions)
![]()
![]()
You can see that it is still the comparison of three values: L, C, and H, where C and H are produced by applying modifying factors to the original Lab values to compensate for perceptual distortions in the colour space. Each difference is squared and the root taken of the sum of the squares, just as in the original Delta E formula.
There is an additional refinement in Delta E(2000) where further adjustments are applied to blue and neutral colours and compensations for lightness, chroma, and hue. This is a much smaller correction than the change from Delta E to Delta E(94).
The good news is that you don’t need to understand or remember any of the details of these equations. Just remember that these are real numbers measuring actual plotted distances between colour samples. Delta E represents the distance between two points in the Lab colour space. Delta E(94) and Delta E(2000) are enhancements, providing improved numbers that more closely match our perception of colour differences.
Media Attributions
- Delta E in Lab Colour Space by Ken Jeffrey