3.6: What Is the Skin Effect? The Skin Depth of Copper in Electrical Engineering

Last updated
Save as PDF

Page ID: 1399

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

What Is the Skin Effect?

As previously mentioned, the skin effect is where alternating current tends to avoid travel through the center of a solid conductor, limiting itself to conduction near the surface. This effectively limits the cross-sectional conductor area available to carry alternating electron flow, increasing the resistance of that conductor above what it would normally be for direct current: (Figure below)

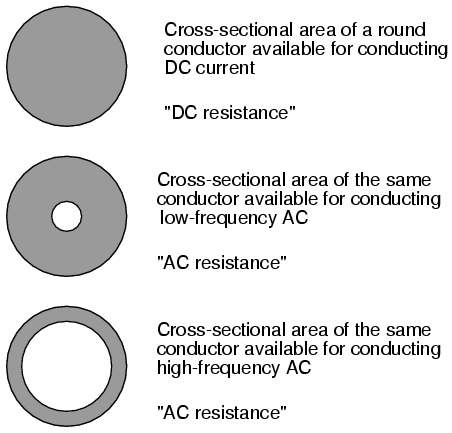
Skin effect: skin depth decreases with increasing frequency.

The electrical resistance of the conductor with all its cross-sectional area in use is known as the “DC resistance.” The “AC resistance” of the same conductor refers to a higher figure resulting from the skin effect. As you can see, at high frequencies the AC current avoids travel through most of the conductor’s cross-sectional area. For the purpose of conducting current, the wire might as well be hollow!

Hollow Conductors in RF Applications

In some radio applications (antennas, most notably) this effect is exploited. Since radio-frequency (“RF”) AC currents wouldn’t travel through the middle of a conductor anyway, why not just use hollow metal rods instead of solid metal wires and save both weight and cost? (Figure below) Most antenna structures and RF power conductors are made of hollow metal tubes for this reason.

In the following photograph, you can see some large inductors used in a 50 kW radio transmitting circuit. The inductors are hollow copper tubes coated with silver, for excellent conductivity at the “skin” of the tube:

High power inductors formed from hollow tubes.

How Wire Gauge Affects Frequency and Effective Resistance

The degree to which frequency affects the effective resistance of a solid wire conductor is impacted by the gauge of that wire. As a rule, large-gauge wires exhibit a more pronounced skin effect (change in resistance from DC) than small-gauge wires at any given frequency. The equation for approximating skin effect at high frequencies (greater than 1 MHz) is as follows:

\[R_{A C}=\left(R_{D C}\right)(k) \sqrt{f} \label{1}\]

where

\(R_{AC}\) is the AC resistance at a given frequency (\(f\))
\(R_{DC}\) is the resistance at zero frequency (e.g., DC)
\(k\) is the wire-gague factor (see table below)
\(f\) is the frequency of AC in MHZ

The table below gives approximate values of “k” factor for various round wire sizes.

Table 1: “k” factor for various AWG wire sizes.

Example \(\PageIndex{1}\)

What is the AC (effective) resistance of a length of number 10-gauge wire with a DC end-to-end resistance of 25 Ω at a frequency of 10 MHz?

Solution

This is a direct application of Equation \ref{1}

\[\begin{align*} R_{A C} &=\left(R_{D C}\right)(k) \sqrt{f} \\[4pt] &=(25 \Omega)(27.6) \sqrt{10} \\[4pt] &=2.182 \mathrm{k} \Omega \end{align*}\]

Hence, this wire would have an AC (effective) resistance of 2.182 kΩ.