6.1: An Electric Pendulum
- Page ID
- 1415
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capacitors store energy in the form of an electric field, and electrically manifest that stored energy as a potential: static voltage. Inductors store energy in the form of a magnetic field, and electrically manifest that stored energy as a kinetic motion of electrons: current. Capacitors and inductors are flip-sides of the same reactive coin, storing and releasing energy in complementary modes. When these two types of reactive components are directly connected together, their complementary tendencies to store energy will produce an unusual result.
If either the capacitor or inductor starts out in a charged state, the two components will exchange energy between them, back and forth, creating their own AC voltage and current cycles. If we assume that both components are subjected to a sudden application of voltage (say, from a momentarily connected battery), the capacitor will very quickly charge and the inductor will oppose change in current, leaving the capacitor in the charged state and the inductor in the discharged state: (Figure below)
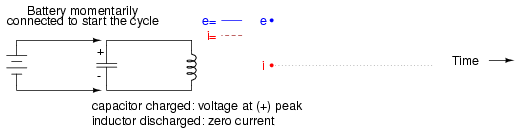
Capacitor charged: voltage at (+) peak, inductor discharged: zero current.
The capacitor will begin to discharge, its voltage decreasing. Meanwhile, the inductor will begin to build up a “charge” in the form of a magnetic field as current increases in the circuit: (Figure below)
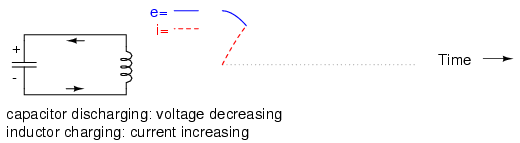 Capacitor discharging: voltage decreasing, Inductor charging: current increasing.
Capacitor discharging: voltage decreasing, Inductor charging: current increasing.
The inductor, still charging, will keep electrons flowing in the circuit until the capacitor has been completely discharged, leaving zero voltage across it: (Figure below)
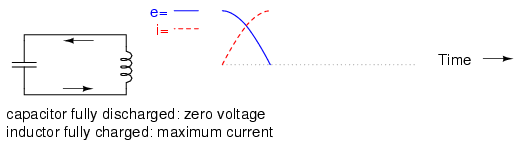
Capacitor fully discharged: zero voltage, inductor fully charged: maximum current.
The inductor will maintain current flow even with no voltage applied. In fact, it will generate a voltage (like a battery) in order to keep current in the same direction. The capacitor, being the recipient of this current, will begin to accumulate a charge in the opposite polarity as before: (Figure below)
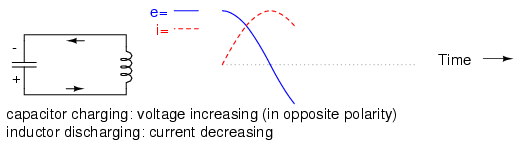 Capacitor charging: voltage increasing (in opposite polarity), inductor discharging: current decreasing.
When the inductor is finally depleted of its energy reserve and the electrons come to a halt, the capacitor will have reached full (voltage) charge in the opposite polarity as when it started: (Figure below)
Capacitor charging: voltage increasing (in opposite polarity), inductor discharging: current decreasing.
When the inductor is finally depleted of its energy reserve and the electrons come to a halt, the capacitor will have reached full (voltage) charge in the opposite polarity as when it started: (Figure below)
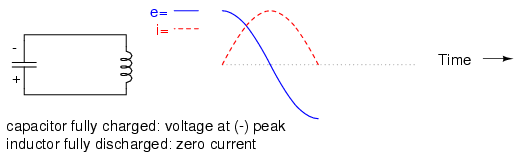
Capacitor fully charged: voltage at (-) peak, inductor fully discharged: zero current.
Now we’re at a condition very similar to where we started: the capacitor at full charge and zero current in the circuit. The capacitor, as before, will begin to discharge through the inductor, causing an increase in current (in the opposite direction as before) and a decrease in voltage as it depletes its own energy reserve: (Figure below)
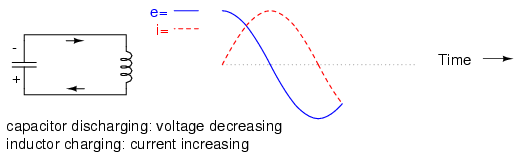
Capacitor discharging: voltage decreasing, inductor charging: current increasing.
Eventually the capacitor will discharge to zero volts, leaving the inductor fully charged with full current through it: (Figure below)
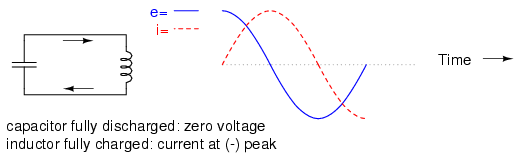
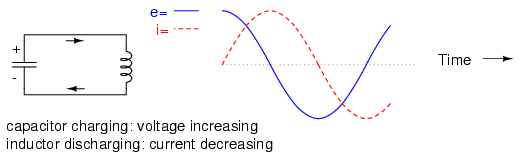
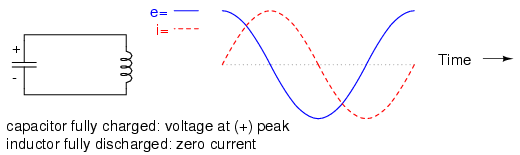
This oscillation will continue with steadily decreasing amplitude due to power losses from stray resistances in the circuit, until the process stops altogether. Overall, this behavior is akin to that of a pendulum: as the pendulum mass swings back and forth, there is a transformation of energy taking place from kinetic (motion) to potential (height), in a similar fashion to the way energy is transferred in the capacitor/inductor circuit back and forth in the alternating forms of current (kinetic motion of electrons) and voltage (potential electric energy).
At the peak height of each swing of a pendulum, the mass briefly stops and switches directions. It is at this point that potential energy (height) is at a maximum and kinetic energy (motion) is at zero. As the mass swings back the other way, it passes quickly through a point where the string is pointed straight down. At this point, potential energy (height) is at zero and kinetic energy (motion) is at maximum. Like the circuit, a pendulum’s back-and-forth oscillation will continue with a steadily dampened amplitude, the result of air friction (resistance) dissipating energy. Also like the circuit, the pendulum’s position and velocity measurements trace two sine waves (90 degrees out of phase) over time: (Figure below)
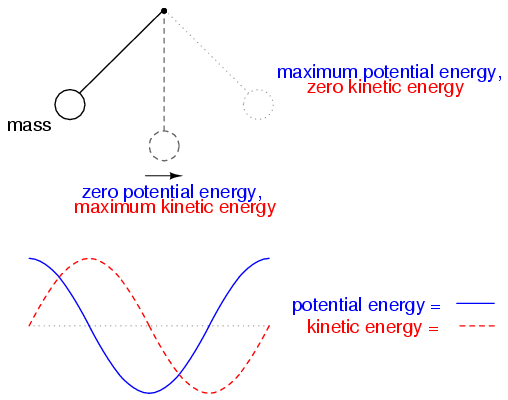
In physics, this kind of natural sine-wave oscillation for a mechanical system is called Simple Harmonic Motion (often abbreviated as “SHM”). The same underlying principles govern both the oscillation of a capacitor/inductor circuit and the action of a pendulum, hence the similarity in effect. It is an interesting property of any pendulum that its periodic time is governed by the length of the string holding the mass, and not the weight of the mass itself. That is why a pendulum will keep swinging at the same frequency as the oscillations decrease in amplitude. The oscillation rate is independent of the amount of energy stored in it.
The same is true for the capacitor/inductor circuit. The rate of oscillation is strictly dependent on the sizes of the capacitor and inductor, not on the amount of voltage (or current) at each respective peak in the waves. The ability for such a circuit to store energy in the form of oscillating voltage and current has earned it the name tank circuit. Its property of maintaining a single, natural frequency regardless of how much or little energy is actually being stored in it gives it special significance in electric circuit design.
However, this tendency to oscillate, or resonate, at a particular frequency is not limited to circuits exclusively designed for that purpose. In fact, nearly any AC circuit with a combination of capacitance and inductance (commonly called an “LC circuit”) will tend to manifest unusual effects when the AC power source frequency approaches that natural frequency. This is true regardless of the circuit’s intended purpose.
If the power supply frequency for a circuit exactly matches the natural frequency of the circuit’s LC combination, the circuit is said to be in a state of resonance. The unusual effects will reach maximum in this condition of resonance. For this reason, we need to be able to predict what the resonant frequency will be for various combinations of L and C, and be aware of what the effects of resonance are.
Review
- A capacitor and inductor directly connected together form something called a tank circuit, which oscillates (or resonates) at one particular frequency. At that frequency, energy is alternately shuffled between the capacitor and the inductor in the form of alternating voltage and current 90 degrees out of phase with each other.
- When the power supply frequency for an AC circuit exactly matches that circuit’s natural oscillation frequency as set by the L and C components, a condition of resonance will have been reached.


