6.5: Resonance in Series-Parallel Circuits
- Page ID
- 1422
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In simple reactive circuits with little or no resistance, the effects of radically altered impedance will manifest at the resonance frequency predicted by the equation given earlier. In a parallel (tank) LC circuit, this means infinite impedance at resonance. In a series LC circuit, it means zero impedance at resonance:
\[f_{resonant} = \dfrac{1}{2\pi \sqrt{LC}}\]
However, as soon as significant levels of resistance are introduced into most LC circuits, this simple calculation for resonance becomes invalid.
On this page, we’ll take a look at several LC circuits with added resistance, using the same values for capacitance and inductance as before: 10 µF and 100 mH, respectively.
Calculating the Resonant Frequency of a High-Resistance Circuit
According to our simple equation above, the resonant frequency should be 159.155 Hz. Watch, though, where current reaches maximum or minimum in the following SPICE analyses:
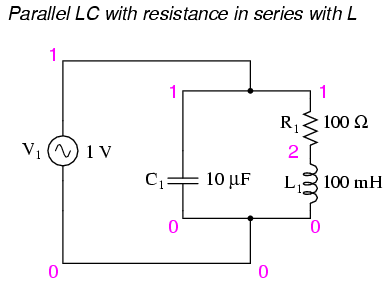
Parallel LC circuit with resistance in series with L.
resonant circuit v1 1 0 ac 1 sin c1 1 0 10u r1 1 2 100 l1 2 0 100m .ac lin 20 100 200 .plot ac i(v1) .end
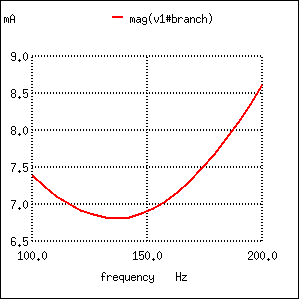
Resistance in series with L produces minimum current at 136.8 Hz instead of calculated 159.2 Hz
Minimum current at 136.8 Hz instead of 159.2 Hz!
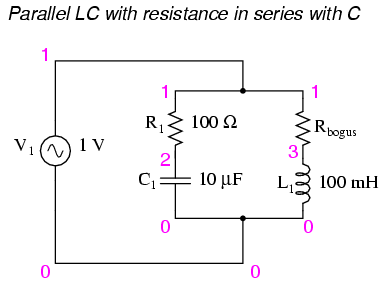
Parallel LC with resistance in serieis with C.
Here, an extra resistor (Rbogus) (see the figure below) is necessary to prevent SPICE from encountering trouble in analysis. SPICE can’t handle an inductor connected directly in parallel with any voltage source or any other inductor, so the addition of a series resistor is necessary to “break up” the voltage source/inductor loop that would otherwise be formed. This resistor is chosen to be a very low value for minimum impact on the circuit’s behavior.
Series LC Circuits
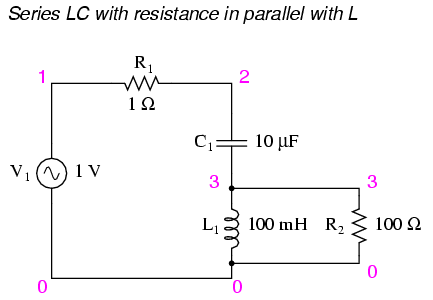
Switching our attention to series LC circuits, (see the figure below) we experiment with placing significant resistances in parallel with either L or C. In the following series circuit examples, a 1 Ω resistor (R1) is placed in series with the inductor and capacitor to limit total current at resonance. The “extra” resistance inserted to influence resonant frequency effects is the 100 Ω resistor, R2. The results are shown in the figure below.
.png?revision=1)
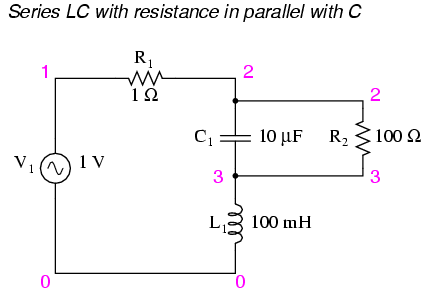
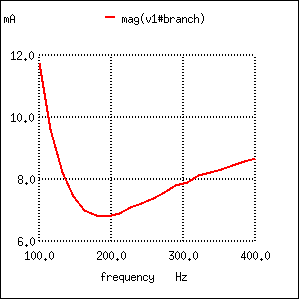
Series LC resonant circuit with resistance in parallel with C.
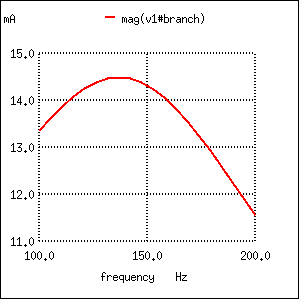
Resistance in parallel with C in series resonant circuit shifts current maximum from calculated 159.2 Hz to about 136.8 Hz.
Antiresonance in LC Circuits
The tendency for added resistance to skew the point at which impedance reaches a maximum or minimum in an LC circuit is called antiresonance. The astute observer will notice a pattern between the four SPICE examples given above, in terms of how resistance affects the resonant peak of a circuit:
Parallel (“tank”) LC circuit:
- R in series with L: resonant frequency shifted down
- R in series with C: resonant frequency shifted up
Series LC circuit:
- R in parallel with L: resonant frequency shifted up
- R in parallel with C: resonant frequency shifted down
Again, this illustrates the complementary nature of capacitors and inductors: how resistance in series with one creates an antiresonance effect equivalent to resistance in parallel with the other. If you look even closer to the four SPICE examples given, you’ll see that the frequencies are shifted by the same amount, and that the shape of the complementary graphs are mirror-images of each other!
Antiresonance is an effect that resonant circuit designers must be aware of. The equations for determining antiresonance “shift” are complex, and will not be covered in this brief lesson. It should suffice the beginning student of electronics to understand that the effect exists, and what its general tendencies are.
The Skin Effect
Added resistance in an LC circuit is no academic matter. While it is possible to manufacture capacitors with negligible unwanted resistances, inductors are typically plagued with substantial amounts of resistance due to the long lengths of wire used in their construction. What is more, the resistance of wire tends to increase as frequency goes up, due to a strange phenomenon known as the skin effect where AC current tends to be excluded from travel through the very center of a wire, thereby reducing the wire’s effective cross-sectional area. Thus, inductors not only have resistance, but changing, frequency-dependent resistance at that.
Added Resistance in Circuits
As if the resistance of an inductor’s wire weren’t enough to cause problems, we also have to contend with the “core losses” of iron-core inductors, which manifest themselves as added resistance in the circuit. Since iron is a conductor of electricity as well as a conductor of magnetic flux, changing flux produced by alternating current through the coil will tend to induce electric currents in the core itself (eddy currents). This effect can be thought of as though the iron core of the transformer were a sort of secondary transformer coil powering a resistive load: the less-than-perfect conductivity of the iron metal. This effects can be minimized with laminated cores, good core design and high-grade materials, but never completely eliminated.
RLC Circuits
One notable exception to the rule of circuit resistance causing a resonant frequency shift is the case of series resistor-inductor-capacitor (“RLC”) circuits. So long as all components are connected in series with each other, the resonant frequency of the circuit will be unaffected by the resistance. (Figure below) The resulting plot is shown in (Figure below).
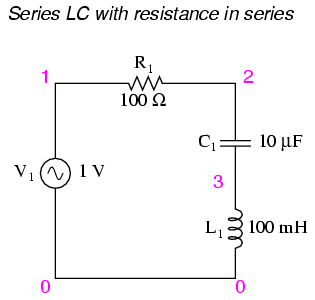
Series LC with resistance in series.
Maximum current at 159.2 Hz once again!
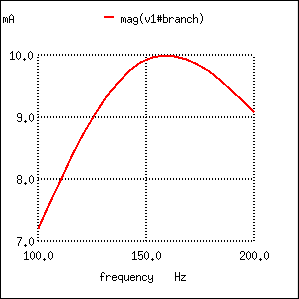
Resistance in series resonant circuit leaves current maximum at calculated 159.2 Hz, broadening the curve.
Note that the peak of the current graph (Figure below) has not changed from the earlier series LC circuit (the one with the 1 Ω token resistance in it), even though the resistance is now 100 times greater. The only thing that has changed is the “sharpness” of the curve. Obviously, this circuit does not resonate as strongly as one with less series resistance (it is said to be “less selective”), but at least it has the same natural frequency!
Antiresonance’s Dampening Effect
It is noteworthy that antiresonance has the effect of dampening the oscillations of free-running LC circuits such as tank circuits. In the beginning of this chapter we saw how a capacitor and inductor connected directly together would act something like a pendulum, exchanging voltage and current peaks just like a pendulum exchanges kinetic and potential energy. In a perfect tank circuit (no resistance), this oscillation would continue forever, just as a frictionless pendulum would continue to swing at its resonant frequency forever. But frictionless machines are difficult to find in the real world, and so are lossless tank circuits. Energy lost through resistance (or inductor core losses or radiated electromagnetic waves or . . .) in a tank circuit will cause the oscillations to decay in amplitude until they are no more. If enough energy losses are present in a tank circuit, it will fail to resonate at all.
Antiresonance’s dampening effect is more than just a curiosity: it can be used quite effectively to eliminate unwanted oscillations in circuits containing stray inductances and/or capacitances, as almost all circuits do. Take note of the following L/R time delay circuit: (Figure below)
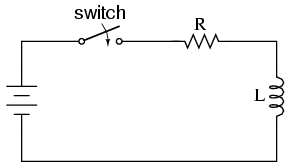
L/R time delay circuit
The idea of this circuit is simple: to “charge” the inductor when the switch is closed. The rate of inductor charging will be set by the ratio L/R, which is the time constant of the circuit in seconds. However, if you were to build such a circuit, you might find unexpected oscillations (AC) of voltage across the inductor when the switch is closed. (Figure below) Why is this? There’s no capacitor in the circuit, so how can we have resonant oscillation with just an inductor, resistor, and battery?
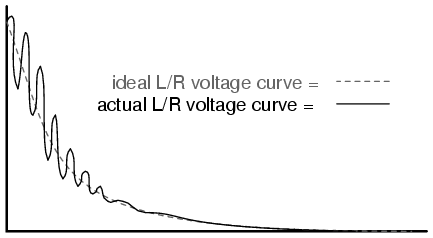
Inductor ringing due to resonance with stray capacitance.
All inductors contain a certain amount of stray capacitance due to turn-to-turn and turn-to-core insulation gaps. Also, the placement of circuit conductors may create stray capacitance. While clean circuit layout is important in eliminating much of this stray capacitance, there will always be some that you cannot eliminate. If this causes resonant problems (unwanted AC oscillations), added resistance may be a way to combat it. If resistor R is large enough, it will cause a condition of antiresonance, dissipating enough energy to prohibit the inductance and stray capacitance from sustaining oscillations for very long.
Interestingly enough, the principle of employing resistance to eliminate unwanted resonance is one frequently used in the design of mechanical systems, where any moving object with mass is a potential resonator. A very common application of this is the use of shock absorbers in automobiles. Without shock absorbers, cars would bounce wildly at their resonant frequency after hitting any bump in the road. The shock absorber’s job is to introduce a strong antiresonant effect by dissipating energy hydraulically (in the same way that a resistor dissipates energy electrically).
Review
- Added resistance to an LC circuit can cause a condition known as antiresonance, where the peak impedance effects happen at frequencies other than that which gives equal capacitive and inductive reactances.
- Resistance inherent in real-world inductors can contribute greatly to conditions of antiresonance. One source of such resistance is the skin effect, caused by the exclusion of AC current from the center of conductors. Another source is that of core losses in iron-core inductors.
- In a simple series LC circuit containing resistance (an “RLC” circuit), resistance does not produce antiresonance. Resonance still occurs when capacitive and inductive reactances are equal.


