12.4: Power Quality Measurement
- Page ID
- 1462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It used to be with large AC power systems that “power quality” was an unheard-of concept, aside from power factor. Almost all loads were of the “linear” variety, meaning that they did not distort the shape of the voltage sine wave, or cause non-sinusoidal currents to flow in the circuit. This is not true anymore. Loads controlled by “nonlinear” electronic components are becoming more prevalent in both home and industry, meaning that the voltages and currents in the power system(s) feeding these loads are rich in harmonics: what should be nice, clean sine-wave voltages and currents are becoming highly distorted, which is equivalent to the presence of an infinite series of high-frequency sine waves at multiples of the fundamental power line frequency.
Excessive harmonics in an AC power system can overheat transformers, cause exceedingly high neutral conductor currents in three-phase systems, create electromagnetic “noise” in the form of radio emissions that can interfere with sensitive electronic equipment, reduce electric motor horsepower output, and can be difficult to pinpoint. With problems like these plaguing power systems, engineers and technicians require ways to precisely detect and measure these conditions.
Power Quality is the general term given to represent an AC power system’s freedom from harmonic content. A “power quality” meter is one that gives some form of harmonic content indication.
A simple way for a technician to determine power quality in their system without sophisticated equipment is to compare voltage readings between two accurate voltmeters measuring the same system voltage: one meter being an “averaging” type of unit (such as an electromechanical movement meter) and the other being a “true-RMS” type of unit (such as a high-quality digital meter). Remember that “averaging” type meters are calibrated so that their scales indicate volts RMS, based on the assumption that the AC voltage being measured is sinusoidal. If the voltage is anything but sinewave-shaped, the averaging meter will not register the proper value, whereas the true-RMS meter always will, regardless of waveshape. The rule of thumb here is this: the greater the disparity between the two meters, the worse the power quality is, and the greater its harmonic content. A power system with good quality power should generate equal voltage readings between the two meters, to within the rated error tolerance of the two instruments.
Another qualitative measurement of power quality is the oscilloscope test: connect an oscilloscope (CRT) to the AC voltage and observe the shape of the wave. Anything other than a clean sine wave could be an indication of trouble: (Figure below)
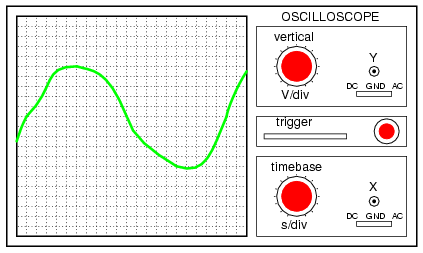
This is a moderately ugly “sine” wave. Definite harmonic content here!
Still, if quantitative analysis (definite, numerical figures) is necessary, there is no substitute for an instrument specifically designed for that purpose. Such an instrument is called a power quality meter and is sometimes better known in electronic circles as a low-frequency spectrum analyzer. What this instrument does is provide a graphical representation on a CRT or digital display screen of the AC voltage’s frequency “spectrum.” Just as a prism splits a beam of white light into its constituent color components (how much red, orange, yellow, green, and blue is in that light), the spectrum analyzer splits a mixed-frequency signal into its constituent frequencies, and displays the result in the form of a histogram: (Figure below)
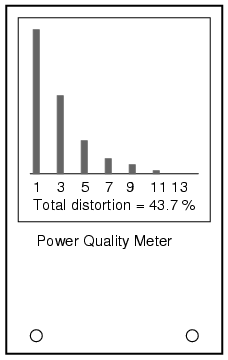
Power quality meter is a low frequency spectrum analyzer.
Each number on the horizontal scale of this meter represents a harmonic of the fundamental frequency. For American power systems, the “1” represents 60 Hz (the 1st harmonic, or fundamental), the “3” for 180 Hz (the 3rd harmonic), the “5” for 300 Hz (the 5th harmonic), and so on. The black rectangles represent the relative magnitudes of each of these harmonic components in the measured AC voltage. A pure, 60 Hz sine wave would show only a tall black bar over the “1” with no black bars showing at all over the other frequency markers on the scale, because a pure sine wave has no harmonic content.
Power quality meters such as this might be better referred to as overtone meters, because they are designed to display only those frequencies known to be generated by the power system. In three-phase AC power systems (predominant for large power applications), even-numbered harmonics tend to be canceled out, and so only harmonics existing in significant measure are the odd-numbered.


