10.8: Monostable Multivibrators
- Page ID
- 1973
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We’ve already seen one example of a monostable multivibrator in use: the pulse detector used within the circuitry of flip-flops, to enable the latch portion for a brief time when the clock input signal transitions from either low to high or high to low. The pulse detector is classified as a monostable multivibrator because it has only one stable state. By stable, I mean a state of output where the device is able to latch or hold to forever, without external prodding. A latch or flip-flop, being a bistable device, can hold in either the “set” or “reset” state for an indefinite period of time. Once its set or reset, it will continue to latch in that state unless prompted to change by an external input. A monostable device, on the other hand, is only able to hold in one particular state indefinitely. Its other state can only be held momentarily when triggered by an external input.
A mechanical analogy of a monostable device would be a momentary contact pushbutton switch, which spring-returns to its normal (stable) position when pressure is removed from its button actuator. Likewise, a standard wall (toggle) switch, such as the type used to turn lights on and off in a house, is a bistable device. It can latch in one of two modes: on or off.
All monostable multivibrators are timed devices. That is, their unstable output state will hold only for a certain minimum amount of time before returning to its stable state. With semiconductor monostable circuits, this timing function is typically accomplished through the use of resistors and capacitors, making use of the exponential charging rates of RC circuits. A comparator is often used to compare the voltage across the charging (or discharging) capacitor with a steady reference voltage, and the on/off output of the comparator used for a logic signal. With ladder logic, time delays are accomplished with time-delay relays, which can be constructed with semiconductor/RC circuits like that just mentioned, or mechanical delay devices which impede the immediate motion of the relay’s armature. Note the design and operation of the pulse detector circuit in ladder logic:
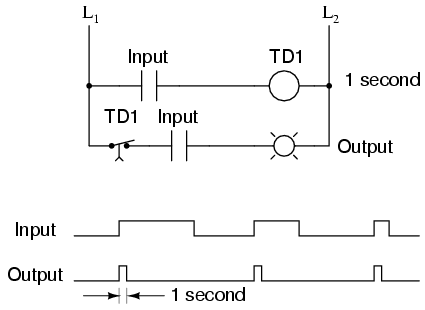
No matter how long the input signal stays high (1), the output remains high for just 1 second of time, then returns to its normal (stable) low state.
For some applications, it is necessary to have a monostable device that outputs a longer pulse than the input pulse which triggers it. Consider the following ladder logic circuit:
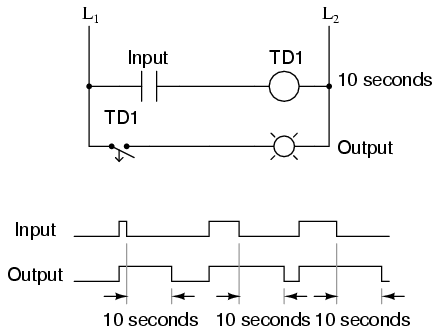
When the input contact closes, TD1 contact immediately closes, and stays closed for 10 seconds after the input contact opens. No matter how short the input pulse is, the output stays high (1) for exactly 10 seconds after the input drops low again. This kind of monostable multivibrator is called a one-shot. More specifically, it is a retriggerable one-shot, because the timing begins after the input drops to a low state, meaning that multiple input pulses within 10 seconds of each other will maintain a continuous high output:
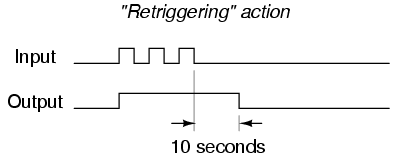
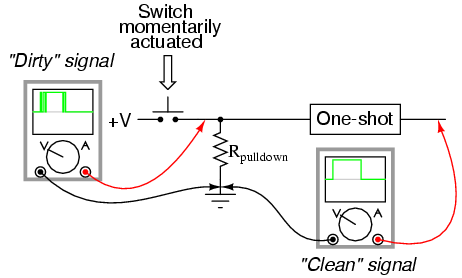
One application for a retriggerable one-shot is that of a single mechanical contact debouncer. As you can see from the above timing diagram, the output will remain high despite “bouncing” of the input signal from a mechanical switch. Of course, in a real-life switch debouncer circuit, you’d probably want to use a time delay of much shorter duration than 10 seconds, as you only need to “debounce” pulses that are in the millisecond range.
What if we only wanted a 10 second timed pulse output from a relay logic circuit, regardless of how many input pulses we received or how long-lived they may be? In that case, we’d have to couple a pulse-detector circuit to the retriggerable one-shot time delay circuit, like this:
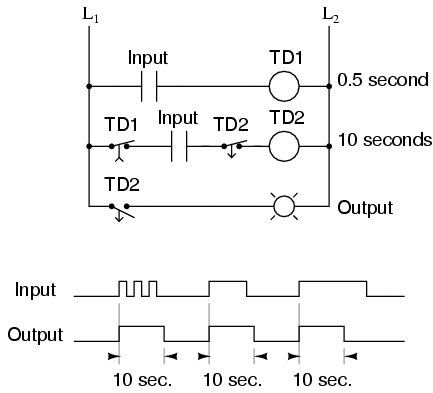
Time delay relay TD1 provides an “on” pulse to time delay relay coil TD2 for an arbitrarily short moment (in this circuit, for at least 0.5 second each time the input contact is actuated). As soon as TD2 is energized, the normally-closed, timed-closed TD2 contact in series with it prevents coil TD2 from being re-energized as long as its timing out (10 seconds). This effectively makes it unresponsive to any more actuations of the input switch during that 10 second period.
Only after TD2 times out does the normally-closed, timed-closed TD2 contact in series with it allow coil TD2to be energized again. This type of one-shot is called a nonretriggerable one-shot.
One-shot multivibrators of both the retriggerable and nonretriggerable variety find wide application in industry for siren actuation and machine sequencing, where an intermittent input signal produces an output signal of a set time.
Review
- A monostable multivibrator has only one stable output state. The other output state can only be maintained temporarily.
- Monostable multivibrators, sometimes called one-shots, come in two basic varieties: retriggerable and nonretriggerable.
- One-shot circuits with very short time settings may be used to debounce the “dirty” signals created by mechanical switch contacts.


