5.3: Half-wave Rectifier
- Page ID
- 1266
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- Low-voltage AC power supply (6-volt output)
- 6-volt battery
- One 1N4001 rectifying diode (Radio Shack catalog # 276-1101)
- Small “hobby” motor, permanent-magnet type (Radio Shack catalog # 273-223 or equivalent)
- Audio detector with headphones
- 0.1 µF capacitor (Radio Shack catalog # 272-135 or equivalent)
The diode need not be an exact model 1N4001. Any of the “1N400X” series of rectifying diodes are suitable for the task, and they are quite easy to obtain.
See the AC experiments chapter for detailed instructions on building the “audio detector” listed here. If you haven’t built one already, you’re missing a simple and valuable tool for experimentation.
A 0.1 µF capacitor is specified for “coupling” the audio detector to the circuit so that only AC reaches the detector circuit. This capacitor’s value is not critical. I’ve used capacitors ranging from 0.27 µF to 0.015 µF with success. Lower capacitor values attenuate low-frequency signals to a greater degree, resulting in less sound intensity from the headphones, so use a greater-value capacitor value if you experience difficulty hearing the tone(s).
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 3, chapter 3: “Diodes and Rectifiers”
LEARNING OBJECTIVES
- Function of a diode as a rectifier
- Permanent-magnet motor operation on AC versus DC power
- Measuring “ripple” voltage with a voltmeter
SCHEMATIC DIAGRAM
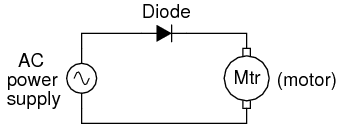
ILLUSTRATION
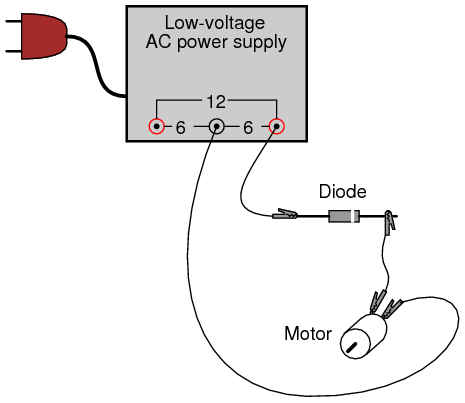
INSTRUCTIONS
Connect the motor to the low-voltage AC power supply through the rectifying diode as shown. The diode only allows current to pass through during one half-cycle of a full positive-and-negative cycle of power supply voltage, eliminating one half-cycle from ever reaching the motor. As a result, the motor only “sees” current in one direction, albeit a pulsating current, allowing it to spin in one direction.
Take a jumper wire and short past the diode momentarily, noting the effect on the motor’s operation:
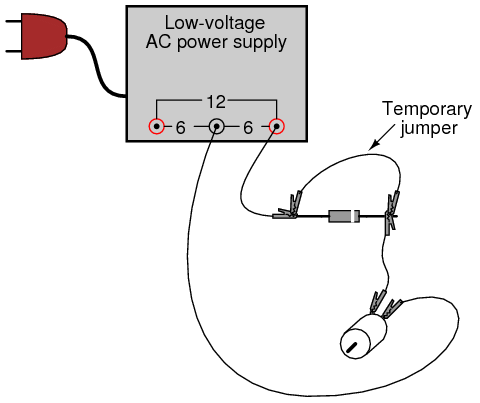
As you can see, permanent-magnet “DC” motors do not function well on alternating current. Remove the temporary jumper wire and reverse the diode’s orientation in the circuit. Note the effect on the motor.
Measure DC voltage across the motor like this:
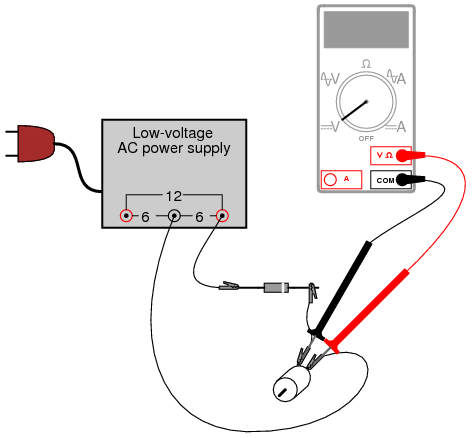
Then, measure AC voltage across the motor as well:
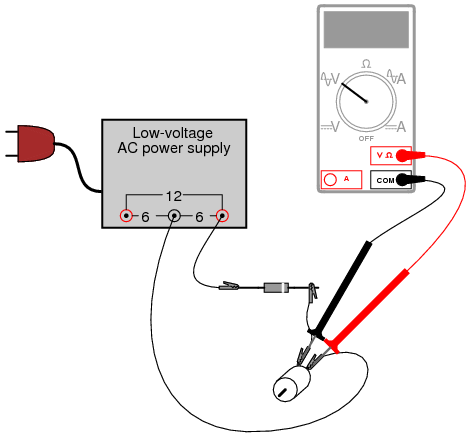
Most digital multimeters do a good job of discriminating AC from DC voltage, and these two measurements show the DC average and AC “ripple” voltages, respectively of the power “seen” by the motor. Ripple voltage is the varying portion of the voltage, interpreted as an AC quantity by measurement equipment although the voltage waveform never actually reverses polarity. Ripple may be envisioned as an AC signal superimposed on a steady DC “bias” or “offset” signal. Compare these measurements of DC and AC with voltage measurements taken across the motor while powered by a battery:
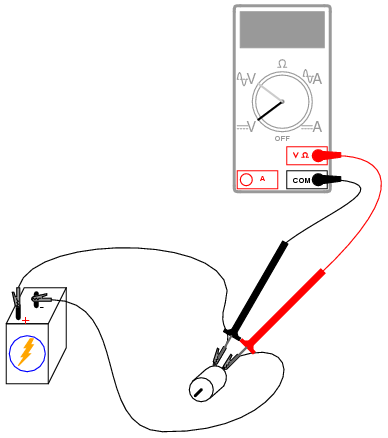
Batteries give very “pure” DC power, and as a result, there should be very little AC voltage measured across the motor in this circuit. Whatever AC voltage is measured across the motor is due to the motor’s pulsating current draw as the brushes make and break contact with the rotating commutator bars. This pulsating current causes pulsating voltages to be dropped across any stray resistances in the circuit, resulting in pulsating voltage “dips” at the motor terminals.
A qualitative assessment of ripple voltage may be obtained by using the sensitive audio detector described in the AC experiments chapter (the same device described as a “sensitive voltage detector” in the DC experiments chapter). Turn the detector’s sensitivity down for low volume, and connect it across the motor terminals through a small (0.1 µF) capacitor, like this:
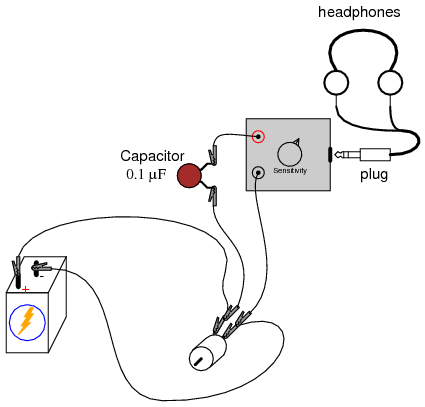
The capacitor acts as a high-pass filter, blocking DC voltage from reaching the detector and allowing easier “listening” of the remaining AC voltage. This is the exact same technique used in oscilloscope circuitry for “AC coupling,” where DC signals are blocked from viewing by a series-connected capacitor. With a battery powering the motor, the ripple should sound like a high-pitched “buzz” or “whine.” Try replacing the battery with the AC power supply and rectifying diode, “listening” with the detector to the low-pitched “buzz” of the half-wave rectified power:
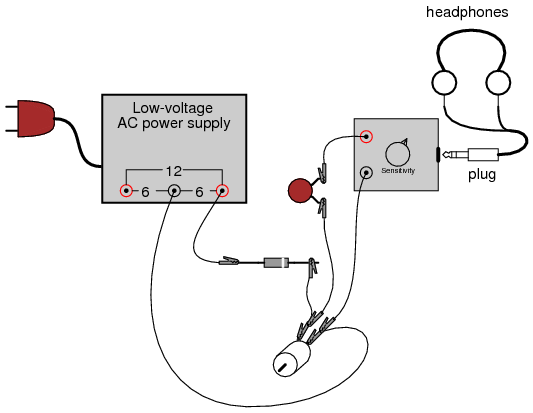
COMPUTER SIMULATION
Schematic with SPICE node numbers:
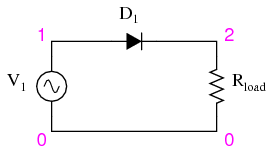
This simulation plots the input voltage as a sine wave and the output voltage as a series of “humps” corresponding to the positive half-cycles of the AC source voltage. The dynamics of a DC motor are far too complex to be simulated using SPICE, unfortunately.
AC source voltage is specified as 8.485 instead of 6 volts because SPICE understands AC voltage in terms of peak value only. A 6 volt RMS sine-wave voltage is actually 8.485 volts peak. In simulations where the distinction between RMS and peak value isn’t relevant, I will not bother with a RMS-to-peak conversion like this. To be truthful, the distinction is not terribly important in this simulation, but I discuss it here for your edification.


