5.12: Common-Emitter Amplifier
- Page ID
- 2181
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- One NPN transistor—model 2N2222 or 2N3403 recommended (Radio Shack catalog # 276-1617 is a package of fifteen NPN transistors ideal for this and other experiments)
- Two 6-volt batteries
- One 10 kΩ potentiometer, single-turn, linear taper (Radio Shack catalog # 271-1715)
- One 1 MΩ resistor
- One 100 kΩ resistor
- One 10 kΩ resistor
- One 1.5 kΩ resistor
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 3, chapter 4: “Bipolar Junction Transistors”
LEARNING OBJECTIVES
- Design of a simple common-emitter amplifier circuit
- How to measure amplifier voltage gain
- The difference between an inverting and a noninverting amplifier
- Ways to introduce negative feedback in an amplifier circuit
SCHEMATIC DIAGRAM
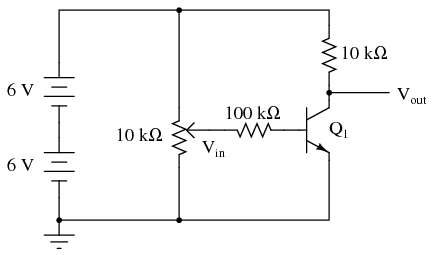
ILLUSTRATION
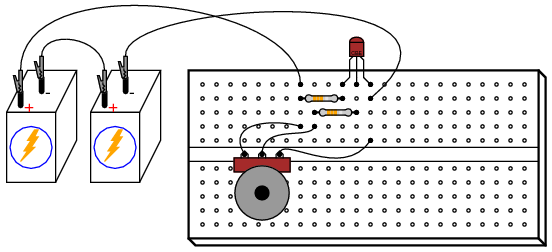
INSTRUCTIONS
Build this circuit and measure output voltage (voltage measured between the transistor’s collector terminal and ground) and input voltage (voltage measured between the potentiometer’s wiper terminal and ground) for several position settings of the potentiometer. I recommend determining the output voltage range as the potentiometer is adjusted through its entire range of motion, then choosing several voltages spanning that output range to take measurements at. For example, if full rotation on the potentiometer drives the amplifier circuit’s output voltage from 0.1 volts (low) to 11.7 volts (high), choose several voltage levels between those limits (1 volt, 3 volts, 5 volts, 7 volts, 9 volts, and 11 volts). Measuring the output voltage with a meter, adjust the potentiometer to obtain each of these predetermined voltages at the output, noting the exact figure for later reference. Then, measure the exact input voltage producing that output voltage, and record that voltage figure as well.
In the end, you should have a table of numbers representing several different output voltages along with their corresponding input voltages. Take any two pairs of voltage figures and calculate voltage gain by dividing the difference in output voltages by the difference in input voltages. For example, if an input voltage of 1.5 volts gives me an output voltage of 7.0 volts and an input voltage of 1.66 volts gives me an output voltage of 1.0 volt, the amplifier’s voltage gain is (7.0 - 1.0)/(1.66 - 1.5), or 6 divided by 0.16: a gain ratio of 37.50.
You should immediately notice two characteristics while taking these voltage measurements: first, that the input-to-output effect is “reversed;” that is, an increasing input voltage results in a decreasing output voltage. This effect is known as signal inversion, and this kind of amplifier as an inverting amplifier. Secondly, this amplifier exhibits a very strong voltage gain: a small change in input voltage results in a large change in output voltage. This should stand in stark contrast to the “voltage follower” amplifier circuit discussed earlier, which had a voltage gain of about 1.
Common-emitter amplifiers are widely used due to their high voltage gain, but they are rarely used in as crude a form as this. Although this amplifier circuit works to demonstrate the basic concept, it is very susceptible to changes in temperature. Try leaving the potentiometer in one position and heating the transistor by grasping it firmly with your hand or heating it with some other source of heat such as an electric hair dryer (WARNING: be careful not to get it so hot that your plastic breadboard melts!). You may also explore temperature effects by cooling the transistor: touch an ice cube to its surface and note the change in output voltage.
When the transistor’s temperature changes, its base-emitter diode characteristics change, resulting in different amounts of base current for the same input voltage. This, in turn, alters the controlled current through the collector terminal, thus affecting output voltage. Such changes may be minimized through the use of signal feedback, whereby a portion of the output voltage is “fed back” to the amplifier’s input so as to have a negative, or canceling, effect on voltage gain. Stability is improved at the expense of voltage gain, a compromise solution, but practical nonetheless.
Perhaps the simplest way to add negative feedback to a common-emitter amplifier is to add some resistance between the emitter terminal and ground so that the input voltage becomes divided between the base-emitter PN junction and the voltage drop across the new resistance:
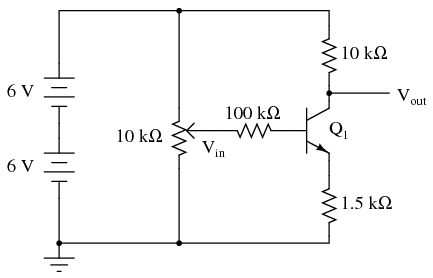
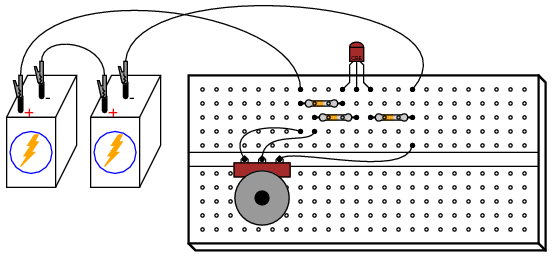
Repeat the same voltage measurement and recording exercise with the 1.5 kΩ resistor installed, calculating the new (reduced) voltage gain. Try altering the transistor’s temperature again and noting the output voltage for a steady input voltage. Does it change more or less than without the 1.5 kΩ resistor?
Another method of introducing negative feedback to this amplifier circuit is to “couple” the output to the input through a high-value resistor. Connecting a 1 MΩ resistor between the transistor’s collector and base terminals works well:
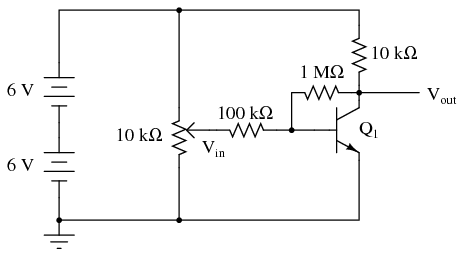
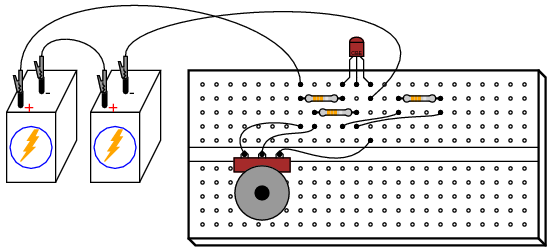
Although this different method of feedback accomplishes the same goal of increased stability by diminishing gain, the two feedback circuits will not behave identically. Note the range of possible output voltages with each feedback scheme (the low and high voltage values obtained with a full sweep of the input voltage potentiometer), and how this differs between the two circuits.
COMPUTER SIMULATION
Schematic with SPICE node numbers:
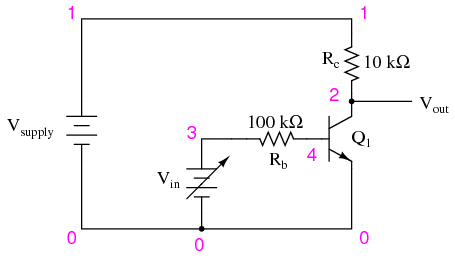
This SPICE simulation sets up a circuit with a variable DC voltage source (vin) as the input signal and measures the corresponding output voltage between nodes 2 and 0. The input voltage is varied, or “swept,” from 0 to 2 volts in 0.05-volt increments. Results are shown on a plot, with the input voltage appearing as a straight line and the output voltage as a “step” figure where the voltage begins and ends level, with a steep change in the middle where the transistor is in its active mode of operation.


