5.17: Simple Op-Amp
- Page ID
- 2186
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- Two 6-volt batteries
- Four NPN transistors—models 2N2222 or 2N3403 recommended (Radio Shack catalog # 276-1617 is a package of fifteen NPN transistors ideal for this and other experiments)
- Two PNP transistors—models 2N2907 or 2N3906 recommended (Radio Shack catalog # 276-1604 is a package of fifteen PNP transistors ideal for this and other experiments)
- Two 10 kΩ potentiometers, single-turn, linear taper (Radio Shack catalog # 271-1715)
- One 270 kΩ resistor
- Three 100 kΩ resistors
- One 10 kΩ resistor
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 3, chapter 4: “Bipolar Junction Transistors”
Lessons In Electric Circuits, Volume 3, chapter 8: “Operational Amplifiers”
LEARNING OBJECTIVES
- Design of a differential amplifier circuit using current mirrors.
- Effects of negative feedback on a high-gain differential amplifier.
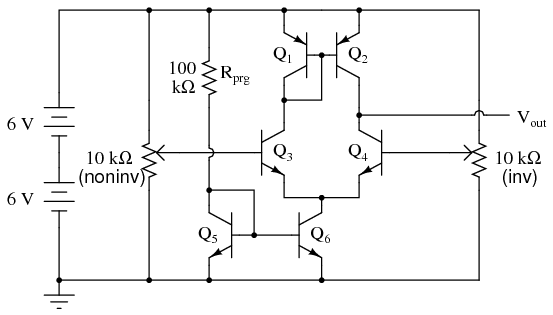
SCHEMATIC DIAGRAM
ILLUSTRATION
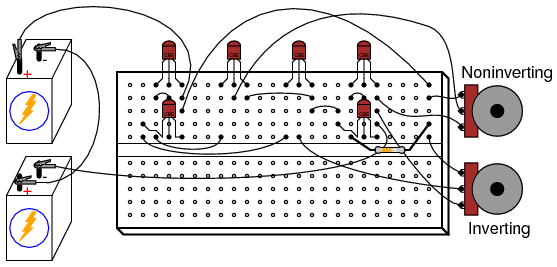
INSTRUCTIONS
This circuit design improves on the differential amplifier shown previously. Rather than use resistors to drop voltage in the differential pair circuit, a set of current mirrors is used instead, the result being higher voltage gain and more predictable performance. With a higher voltage gain, this circuit is able to function as a working operational amplifier or op-amp. Op-amps form the basis of a great many modern analog semiconductor circuits, so understanding the internal workings of an operational amplifier is important.
PNP transistors Q1 and Q2 form a current mirror which tries to keep current split equally through the two differential pair transistors Q3 and Q4. NPN transistors Q5 and Q6 form another current mirror, setting the total differential pair current at a level predetermined by resistor Rprg.
Measure the output voltage (voltage at the collector of Q4 with respect to ground) as the input voltages are varied. Note how the two potentiometers have different effects on the output voltage: one input tends to drive the output voltage in the same direction (noninverting), while the other tends to drive the output voltage in the opposite direction (inverting). You will notice that the output voltage is most responsive to changes in the input when the two input signals are nearly equal to each other.
Once the circuit’s differential response has been proven (the output voltage sharply transitioning from one extreme level to another when one input is adjusted above and below the other input’s voltage level), you are ready to use this circuit as a real op-amp. A simple op-amp circuit called a voltage follower is a good configuration to try first. To make a voltage follower circuit, directly connect the output of the amplifier to its inverting input. This means connecting the collector and base terminals of Q4 together, and discarding the “inverting” potentiometer:
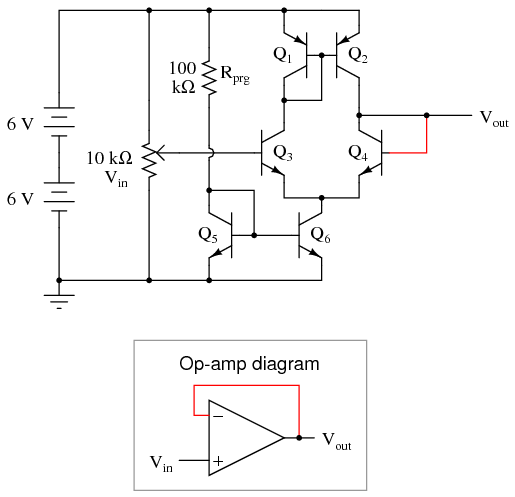
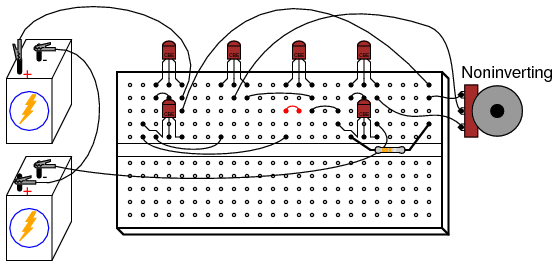
Note the triangular symbol of the op-amp shown in the lower schematic diagram. The inverting and noninverting inputs are designated with (-) and (+) symbols, respectively, with the output terminal at the right apex. The feedback wire connecting output to inverting input is shown in red in the above diagrams.
As a voltage follower, the output voltage should “follow” the input voltage very closely, deviating no more than a few hundredths of a volt. This is a much more precise follower circuit than that of a single common-collector transistor, described in an earlier experiment!
A more complex op-amp circuit is called the noninverting amplifier, and it uses a pair of resistors in the feedback loop to “feedback” a fraction of the output voltage to the inverting input, causing the amplifier to output a voltage equal to some multiple of the voltage at the noninverting input. If we use two equal-value resistors, the feedback voltage will be 1/2 the output voltage, causing the output voltage to become twice the voltage impressed at the noninverting input. Thus, we have a voltage amplifier with a precise gain of 2:
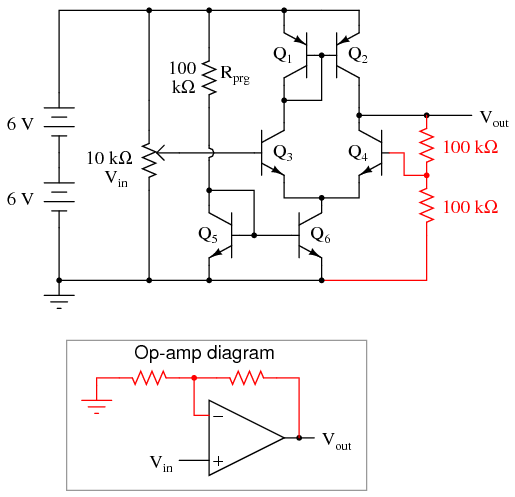
As you test this noninverting amplifier circuit, you may notice slight discrepancies between the output and input voltages. According to the feedback resistor values, the voltage gain should be exactly 2. However, you may notice deviations in the order of several hundredths of a volt between what the output voltage is and what it should be. These deviations are due to imperfections of the differential amplifier circuit and may be greatly diminished if we add more amplification stages to increase the differential voltage gain. However, one way we can maximize the precision of the existing circuit is to change the resistance of Rprg. This resistor sets the lower current mirror’s control point, and in so doing influences many performance parameters of the op-amp. Try substituting difference resistance values, ranging from 10 kΩ to 1 MΩ. Do not use a resistance less than 10 kΩ, or else the current mirror transistors may begin to overheat and thermally “run away.”
Some operational amplifiers available in prepackaged units provide a way for the user to similarly “program” the differential pair’s current mirror and are called programmable op-amps. Most op-amps are not programmable and have their internal current mirror control points fixed by an internal resistance, trimmed to precise value at the factory.


