6.6: Integrator
- Page ID
- 1276
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)PARTS AND MATERIALS
- Four 6 volt batteries
- Operational amplifier, model 1458 recommended (Radio Shack catalog # 276-038)
- One 10 kΩ potentiometer, linear taper (Radio Shack catalog # 271-1715)
- Two capacitors, 0.1 µF each, non-polarized (Radio Shack catalog # 272-135)
- Two 100 kΩ resistors
- Three 1 MΩ resistors
Just about any operational amplifier model will work fine for this integrator experiment, but I’m specifying the model 1458 over the 353 because the 1458 has much higher input bias currents. Normally, high input bias current is a bad characteristic for an op-amp to have in a precision DC amplifier circuit (and especially an integrator circuit!). However, I want the bias current to be high in order that its bad effects may be exaggerated, and so that you will learn one method of counteracting its effects.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 3, chapter 8: “Operational Amplifiers”
LEARNING OBJECTIVES
- Method for limiting the span of a potentiometer
- Purpose of an integrator circuit
- How to compensate for op-amp bias current
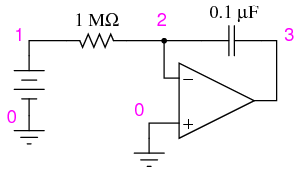
SCHEMATIC DIAGRAM
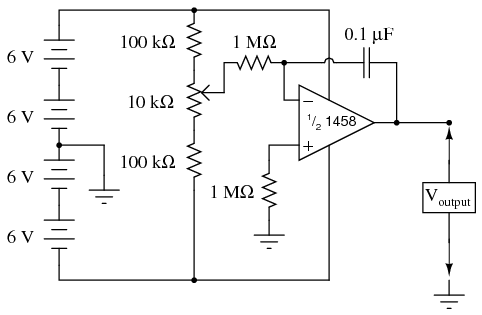
ILLUSTRATION
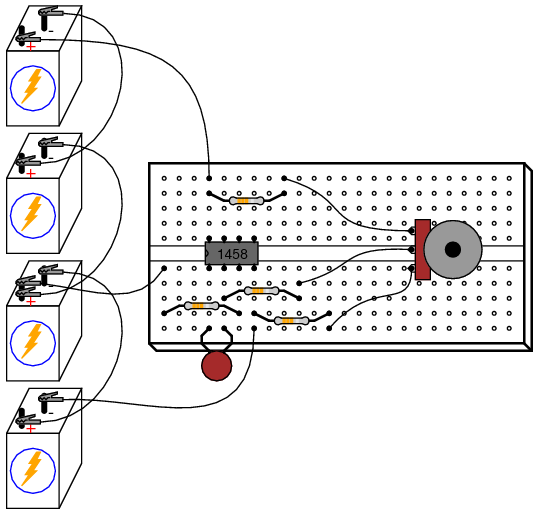
INSTRUCTIONS
As you can see from the schematic diagram, the potentiometer is connected to the “rails” of the power source through 100 kΩ resistors, one on each end. This is to limit the span of the potentiometer so that full movement produces a fairly small range of input voltages for the op-amp to operate on. At one extreme of the potentiometer’s motion, a voltage of about 0.5 volts (with respect the ground point in the middle of the series battery string) will be produced at the potentiometer wiper. At the other extreme of motion, a voltage of about -0.5 volts will be produced. When the potentiometer is positioned dead-center, the wiper voltage should measure zero volts.
Connect a voltmeter between the op-amp’s output terminal and the circuit ground point. Slowly move the potentiometer control while monitoring the output voltage. The output voltage should be changing at a rate established by the potentiometer’s deviation from zero (center) position. To use calculus terms, we would say that the output voltage represents the integral (with respect to time) of the input voltage function. That is, the input voltage level establishes the output voltage rate of change over time. This is precisely the opposite of differentiation, where the derivative of a signal or function is its instantaneous rate of change.
If you have two voltmeters, you may readily see this relationship between input voltage and output voltage rate of change by measuring the wiper voltage (between the potentiometer wiper and ground) with one meter and the output voltage (between the op-amp output terminal and ground) with the other. Adjusting the potentiometer to give zero volts should result in the lowest output voltage rate-of-change. Conversely, the more voltage input to this circuit, the faster its output voltage will change, or “ramp.”
Try connecting the second 0.1 µF capacitor in parallel with the first. This will double the amount of capacitance in the op-amp’s feedback loop. What effect does this have on the circuit’s integration rate for any given potentiometer position?
Try connecting another 1 MΩ resistor in parallel with the input resistor (the resistor connecting the potentiometer wiper to the inverting terminal of the op-amp). This will half the integrator’s input resistance. What effect does this have on the circuit’s integration rate?
Integrator circuits are one of the fundamental “building-block” functions of an analog computer. By connecting integrator circuits with amplifiers, summers, and potentiometers (dividers), almost any differential equation could be modeled, and solutions obtained by measuring voltages produced at various points in the network of circuits. Because differential equations describe so many physical processes, analog computers are used as simulators. Before the advent of modern digital computers, engineers used analog computers to simulate such processes as machinery vibration, rocket trajectory, and control system response. Even though analog computers are considered obsolete by modern standards, their constituent components still work well as learning tools for calculus concepts.
Move the potentiometer until the op-amp’s output voltage is as close to zero as you can get it, and moving as slowly as you can make it. Disconnect the integrator input from the potentiometer wiper terminal and connect it instead to ground, like this:
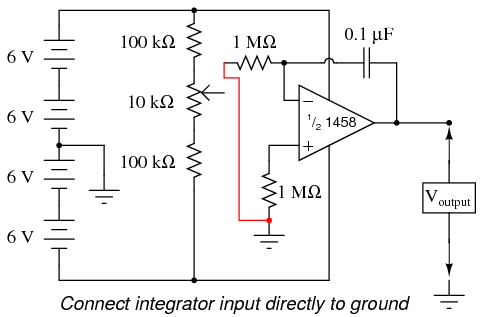
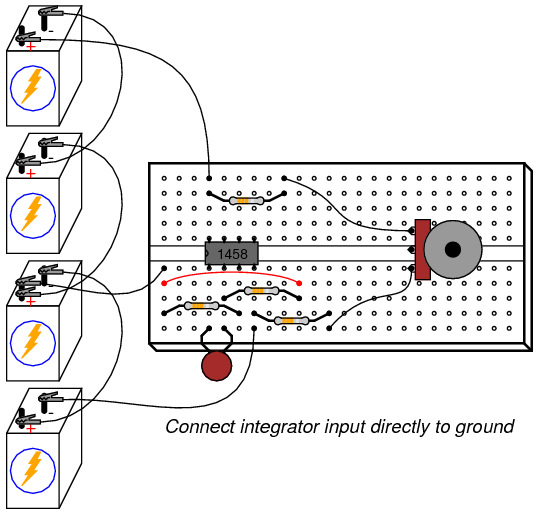
Applying exactly zero voltage to the input of an integrator circuit should, ideally, cause the output voltage rate-of-change to be zero. When you make this change to the circuit, you should notice the output voltage remaining at a constant level or changing very slowly.
With the integrator input still shorted to ground, short past the 1 MΩ resistor connecting the op-amp’s noninverting (+) input to ground. There should be no need for this resistor in an ideal op-amp circuit, so by shorting past it, we will see what function it provides in this very real op-amp circuit:
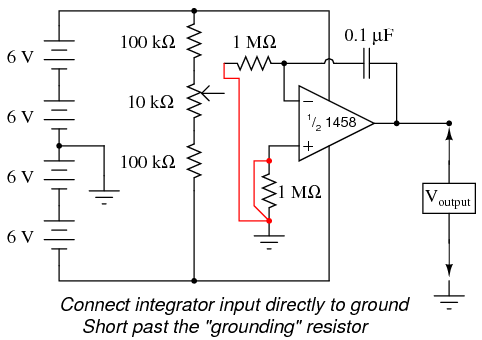
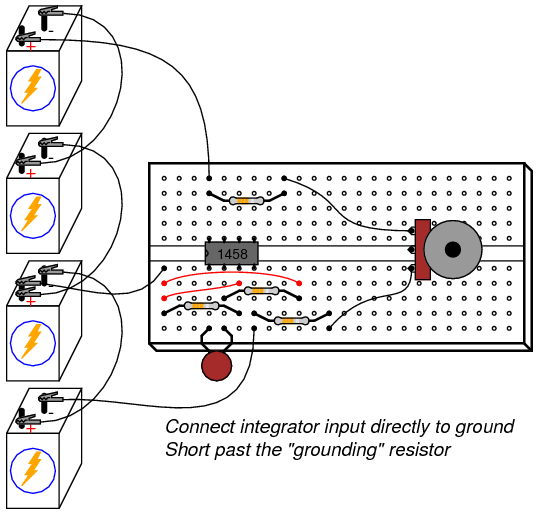
As soon as the “grounding” resistor is shorted with a jumper wire, the op-amp’s output voltage will start to change, or drift. Ideally, this should not happen, because the integrator circuit still has an input signal of zero volts. However, real operational amplifiers have a very small amount of current entering each input terminal called the bias current. These bias currents will drop voltage across any resistance in their path. Since the 1 MΩ input resistor conducts some amount of bias current regardless of input signal magnitude, it will drop voltage across its terminals due to bias current, thus “offsetting” the amount of signal voltage seen at the inverting terminal of the op-amp. If the other (noninverting) input is connected directly to ground as we have done here, this “offset” voltage incurred by voltage drop generated by bias current will cause the integrator circuit to slowly “integrate” as though it were receiving a very small input signal.
The “grounding” resistor is better known as a compensating resistor because it acts to compensate for voltage errors created by bias current. Since the bias currents through each op-amp input terminal are approximately equal to each other, an equal amount of resistance placed in the path of each bias current will produce approximately the same voltage drop. Equal voltage drops seen at the complementary inputs of an op-amp cancel each other out, thus nulling the error otherwise induced by bias current.
Remove the jumper wire shorting past the compensating resistor and notice how the op-amp output returns to a relatively stable state. It may still drift some, most likely due to bias voltage error in the op-amp itself, but that is another subject altogether!
COMPUTER SIMULATION
Schematic with SPICE node numbers: