3.5: Frequency and Alternators
- Page ID
- 2645
In the last chapter, we learned the term cycle means from the point in a waveform to where the waveform starts to repeat itself. When we discuss the term frequency, we are referring to how many cycles can occur in one second. Frequency is measured in hertz (shout out to Heinrich Hertz) or CPS (cycles per second). Two factors affect the frequency in an alternator: rotation speed and the number of poles.
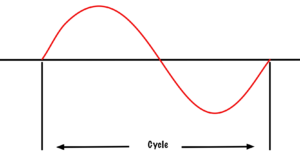
Figure 52. Sine wave cycle
Rotation speed
As the armature rotates through the field, it starts to create a waveform (as we saw in the last chapter). One full mechanical rotation of the armature creates one full sine wave on a two-pole alternator. If the two-pole alternator spins three complete revolutions in one second, it will create three full sine waves in that one second. We would say that the frequency is at three cycles per second or three hertz (as the cool kids say).
A machine’s rotational speed is measured in rotations per minute or RPM. However, we are not concerned with minutes, but rather, with seconds when dealing with frequency. Therefore, RPM must be converted to rotations per second (RPS). As there are 60 seconds in a minute, all we have to do is to divide the RPM by 60 to convert it to RPS.
For example, if the armature is spinning at a rate of 1800 RPM on a two-pole alternator, we can say that it is spinning at 30 rotations per second. If this alternator has two poles, then in one second it will generate 30 cycles of voltage. It then could be said to have a frequency of 30 cycles per second or 30 Hertz. The frequency of an alternator is directly proportional to the rotational speed of the alternator.
Number of Poles
If we add poles to the alternator, we can change the frequency. In a two-pole alternator, Side A of the armature (Figure 53) passes from north to south, and then south to north, to create one complete sine wave. I f we add two more poles, as in Figure 54, then Side A of the armature will move past two north poles and two south poles in one full mechanical revolution.
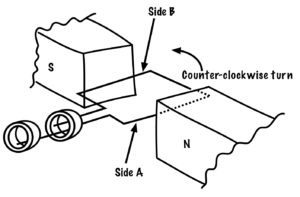
Figure 53. Two pole alternator
Two full sine waves are created in one complete mechanical revolution. If a two-pole alternator creates one cycle of voltage in one second (or one hertz of frequency), a four pole alternator will create two cycles of voltage in one second (or two hertz).
The frequency of an alternator is directly proportional to the number of poles in the alternator.
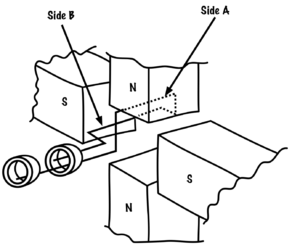
Figure 54. Four pole alternator
Formula time!
Knowing that rotation speed is directly proportional to frequency and that the number of poles is directly proportional to frequency, we can use a formula. The formula looks like this:
\[ f= \dfrac{P}{2} \times \dfrac{N}{60} \tag{Frequency formula}\]
where…
- \(f\) = frequency in hertz
- \(P\) = number of poles
- \(N\) = rotational speed in RPM
We divide the number of poles by two because there will always be a set of two poles. You can’t have a north pole without a south. We divide the RPM by 60 because we are concerned with rotations per second, not rotations per minute. The formula in Figure 56 can be combined to look like this:
\[f = \dfrac{PN}{120} \tag{Combined frequency formula}\]