5.4: Conductance
- Page ID
- 715
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When students first see the parallel resistance equation, the natural question to ask is, “Where did that thing come from?” It is truly an odd piece of arithmetic, and its origin deserves a good explanation.
What is the Difference Between Resistance and Conductance?
Resistance, by definition, is the measure of friction a component presents to the flow of electrons through it. Resistance is symbolized by the capital letter “R” and is measured in the unit of “ohm.” However, we can also think of this electrical property in terms of its inverse: how easy it is for electrons to flow through a component, rather than how difficult. If resistance is the word we use to symbolize the measure of how difficult it is for electrons to flow, then a good word to express how easy it is for electrons to flow would be conductance.
Mathematically, conductance is the reciprocal, or inverse, of resistance:
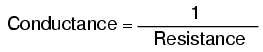
The greater the resistance, the less the conductance, and vice versa. This should make intuitive sense, resistance and conductance being opposite ways to denote the same essential electrical property. If two components’ resistances are compared and it is found that component “A” has one-half the resistance of component “B,” then we could alternatively express this relationship by saying that component “A” is twiceas conductive as component “B.” If component “A” has but one-third the resistance of component “B,” then we could say it is three times more conductive than component “B,” and so on.
Carrying this idea further, a symbol and unit were created to represent conductance. The symbol is the capital letter “G” and the unit is the mho, which is “ohm” spelled backwards (and you didn’t think electronics engineers had any sense of humor!). Despite its appropriateness, the unit of the mho was replaced in later years by the unit of siemens (abbreviated by the capital letter “S”). This decision to change unit names is reminiscent of the change from the temperature unit of degrees Centigrade to degrees Celsius, or the change from the unit of frequency c.p.s. (cycles per second) to Hertz. If you’re looking for a pattern here, Siemens, Celsius, and Hertz are all surnames of famous scientists, the names of which, sadly, tell us less about the nature of the units than the units’ original designations.
As a footnote, the unit of siemens is never expressed without the last letter “s.” In other words, there is no such thing as a unit of “siemen” as there is in the case of the “ohm” or the “mho.” The reason for this is the proper spelling of the respective scientists’ surnames. The unit for electrical resistance was named after someone named “Ohm,” whereas the unit for electrical conductance was named after someone named “Siemens,” therefore it would be improper to “singularize” the latter unit as its final “s” does not denote plurality.
Back to our parallel circuit example, we should be able to see that multiple paths (branches) for current reduces total resistance for the whole circuit, as electrons are able to flow easier through the whole network of multiple branches than through any one of those branch resistances alone. In terms of resistance, additional branches result in a lesser total (current meets with less opposition). In terms of conductance, however, additional branches results in a greater total (electrons flow with greater conductance):
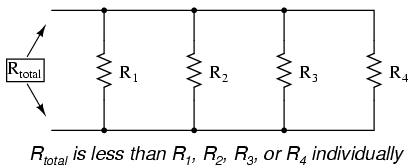
Total Parallel Resistance
Total parallel resistance is less than any one of the individual branch resistances because parallel resistors resist less together than they would separately:
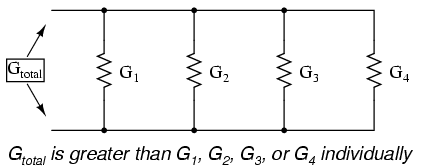
Total Parallel Conductance
Total parallel conductance is greater than any of the individual branch conductances because parallel resistors conduct better together than they would separately:
To be more precise, the total conductance in a parallel circuit is equal to the sum of the individual conductances:
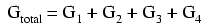
If we know that conductance is nothing more than the mathematical reciprocal (1/x) of resistance, we can translate each term of the above formula into resistance by substituting the reciprocal of each respective conductance:
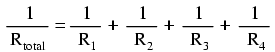
Solving the above equation for total resistance (instead of the reciprocal of total resistance), we can invert (reciprocate) both sides of the equation:
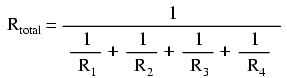
So, we arrive at our cryptic resistance formula at last! Conductance (G) is seldom used as a practical measurement, and so the above formula is a common one to see in the analysis of parallel circuits.
Review
- Conductance is the opposite of resistance: the measure of how easy it is for electrons to flow through something.
- Conductance is symbolized with the letter “G” and is measured in units of mhos or Siemens.
- Mathematically, conductance equals the reciprocal of resistance: G = 1/R


