7.3: Flow Rate

Last updated
Save as PDF

Page ID: 7098

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Flow is the path that a certain liquid (water) takes for a specific time. It is commonly referred to as Flow Rate. A garden hose, a water main, an aqueduct, a gutter, have flow rates. You must know the area of the vessel or container that is flowing the liquid and you must also know the velocity that the liquid is moving. Flow Rate is simply expressed as volume over time.

\[\dfrac{\text { Volume }}{\text { Time }} \nonumber \]

The volume can be gallons, million gallons, cubic feet or any other volume unit. The time can be any time such as, seconds, minutes, hours, etc. However, when solving Flow Rate ALWAYS use the UNTIS – CUBIC FEET PER SECOND, where Q represents Flow Rate.

Expressed as

\[\mathrm{Q}=\dfrac{\text { Volume }}{\text { Time }}=\dfrac{\text { cubic feet }}{\text { second }} \nonumber \]

In order to calculate a Flow Rate, you need to know the Area of the vessel that the liquid is traveling through and the Velocity in which the liquid is traveling. The formula for Flow Rate is

\[\mathrm{Q}=\mathrm{A} \times \mathrm{V} \nonumber \]

Where the Area is expressed as – \(0.785 \times D^2 \) (for circles) - \(L \times H\) (for rectangles) and \(\dfrac{b 1+b 2}{2} \times H\) (for trapezoids)

And

Where Velocity is expressed as – \(\dfrac{\text { Distance }}{\text { Time }}\)

The UNITS for AREA should always be in SQUARE FEET and the UNITS for VELOCITY should always be in FEET PER SECOND.

Therefore, the equation should look like this

\[\dfrac{\text { cubic }}{\text { feet }}=\dfrac{\mathrm{ft}^{2}}{1} \times \dfrac{\mathrm{ft}}{\text { second }} \quad \rightarrow \quad \dfrac{\mathrm{ft} \times \mathrm{ft} \times \mathrm{ft}}{\text { second }}=\dfrac{\mathrm{ft} \times \mathrm{ft}}{1} \times \dfrac{\mathrm{ft}}{\text { second }} \nonumber \]

If you like using the “Pie Wheel” the following can be applied for Flow Rate.

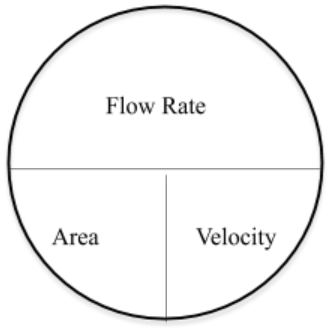
Exercise 7.3

What is the pressure in pounds per square inch at the bottom of a 45 foot tall water storage tank?
An 80 foot tall standpipe is ¾ full. What is the pressure in psi at the bottom?
A 30 foot water tank has a pressure gauge installed 2 feet from the bottom of the tank. If the pressure gauge reads 11 psi, what is the level in the tank?
A 12” pipeline is flowing water at a velocity of 3.5 fps. What is the corresponding flow rate?
A 36” diameter pipe is flowing water at a velocity of 5 fps. How many gallons of water will flow through it in 2 hours?
An 18” pipe is flowing 1,500 gpm. What is the velocity?
What is the area of a box culvert that is flowing 4.5 MGD at a velocity of 2.45 fps?
An 8” diameter pipe is flowing water at a velocity of 7.65 fps. What is the flow rate in gallons per minute?
A 28 foot tall water tank is sitting on a 75 foot tall hill. What is the pressure in a home at the bottom of the hill? (Assume the pressure gauge is 3 feet from the bottom of the home and the tank is full)
What is the velocity through a 20” diameter pipe that flows 2.5 MGD?
A home that is receiving water from a water tank that is on top of a 115 foot hill has a pressure of 57 psi. What is the water level in the tank?
What is the area of a pipe that flows 2,550 gpm at a velocity of 5 fps?