8.1: The “Pound Formula”
- Page ID
- 7099
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When solving the “Pound” formula the following two formulas are used.
The first formula is used when you are calculating chemical dosage on a volume of water, for example a tank, reservoir, or pipeline.
\[\dfrac{\mathrm{MG}}{1} \times \dfrac{8.34 \mathrm{lbs}}{\mathrm{gal}} \times \dfrac{\text { parts }}{\text { millionparts }}=\dfrac{\mathrm{lbs}}{1} \nonumber \]
The second formula is used when you are calculating chemical dosage on a flow rate, for example through a pipeline, in a channel, or through a treatment facility.
\[\dfrac{\mathrm{MG}}{\mathrm{D}} \times \dfrac{8.34 \mathrm{lbs}}{\mathrm{gal}} \times \dfrac{\text { parts }}{\text { millionparts }}=\dfrac{\mathrm{lbs}}{\mathrm{day}} \nonumber \]
Note that the only difference between the two formulas is the unit for time. It is also important to note that the formula uses specific units for volume and flow…MILLION GALLONS and MILLION GALLONS PER DAY.
Therefore if you are given a volume in cubic feet, gallons, acre-feet or some other unit, you must convert to million gallons.
The same holds true for flow rates. If you are given a flow rate in cubic feet per second, gallons per minute, acre-feet per year or some other unit, you must convert to million gallons per day.
The following charts are helpful in illustrating how to use the pound formula. Look at the horizontal line as a division sign. Anything above the line is divided by anything below the line. Everything below the line (that are next to each other) would be multiplied together.
Here is an example.
Example \(\PageIndex{1}\)
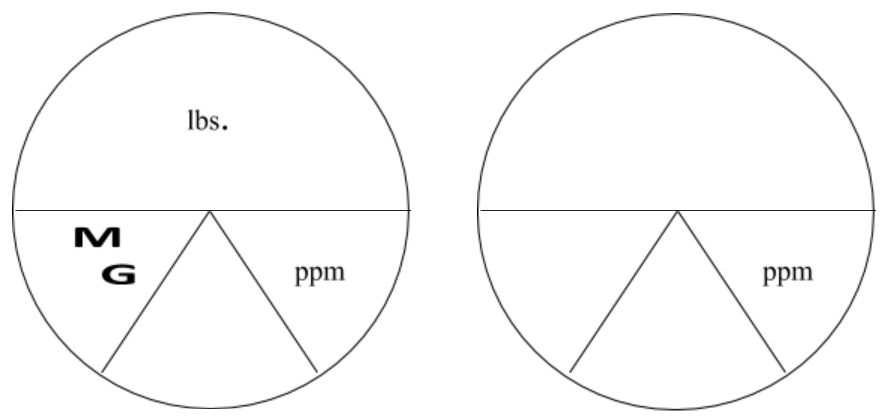
MG(D) and ppm are the two variables below the line. Therefore, they would be multiplied by each other and multiplied by 8.34 lbs./gallon. Since lbs or lbs/day are above the line then you would divide the product of the values below the line.
In this class we will assume that any chemical we are using is in its pure form. In other words there is no adjustment for a lesser concentration form of a chemical. When chlorine is used, it is 100% chlorine.
In addition to drinking water treatment, wastewater treatment uses this same formula to calculate the chemical dosage needed to add certain chemicals to wastewater. Also, this formula is used to determine the amount of “waste” present in wastewater. A common way to measure the amount of organic waste is by the Biochemcial Oxygen Demand (BOD) test. Wastewater has a large amount of organic material that would put a certain demand on an aquatic system by depleting the available oxygen. The results of the test are typically expressed as mg/L or ppm and can be used in the “pound formula.” The following questions cover both drinking water and wastewater treatment processes.
Exercises 8.1
- How many pounds of chlorine are needed to dose 1 MG of water to 2 ppm?
- How many pounds of chlorine are needed to dose 2,200,000 gallons of water to a concentration of 3.5 mg/L?
- Dry Alum is added at a rate of 150 lb/day in a treatment plant operating at a rate of 16 MGD. What is the dosage in milligrams per liter?
- How many gallons of water can be treated to a dosage of 10 ppm with 150 pounds of chlorine?
- A wastewater treatment plant has a primary tank that can hold 2.5 MG. If the BOD test results are 450 mg/L, how many pounds of BOD are in the tank?
- An operator added 75 pounds of chlorine to a water storage tank that has a 100 foot diameter and is 30 feet tall. The tank was only half full. What was the dosage?
- A wastewater treatment plant treats 37,500 lbs of BOD per day. If the average daily flow is 8 MGD, what is the BOD concentration?
- A well is flowing at a rate of 1,600 gpm and requires a dosage of 0.5 mg/L. How pounds of chlorine are needed per day?
- An aeration tank receives a flow rate of 4,500 gpm. If the BOD concentration is 210mg/L, how many pounds of BOD are loading the aeration tank?
- A treatment plant operates at a rated capacity of 15 MGD and maintains a constant 1.25 mg/L chlorine dosage. How many pounds of chlorine are needed per year?
- In question 10, what is the annual budget for chlorine if the cost is $1.65 per pound?
- A wastewater treatment plant receives an average daily flow of 9.5 MGD. If the BOD test results are 320 mg/L, how many pounds of BOD does the treatment plant receive in a single day?
- A water tank has a 150 foot diameter and is 35 feet tall. If 200 pounds of chlorine were added to it, what is the dosage?
- How pounds of ferric chloride are needed to treat a basin that is 120 feet long, 30 feet wide, and 15 feet deep to a dosage of 3.25 mg/L?

