9.1: Detention Time

Last updated
Save as PDF

Page ID: 7102

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Detention Time is the amount of time it takes for a molecule of water to travel a certain distance. In a sedimentation basin it is the time it takes for a particle to travel across the basin. Water treatment operators calculate detention times for settling basins, flocculation basins, or rapid mixing chambers. The term “Contact Time” can also be applied using this formula. Contact Time is not to be confused with CT (Concentration Time). Contact Time is best described as the time a certain chemical is in contact with water. For instance, if you add chlorine to a water supply you can ask yourself “how long is it in contact with the water before a customer drinks the water?” For reference, Detention Times are commonly expressed in hours. However, as you will see when solving for Detention Time the resulting answer will not be in hours and will have to be converted.

Figure \(\PageIndex{1}\): Treatment Process Example

The following formula is used for calculating detention times.

\[\mathrm{Dt}=\dfrac{\text { Volume }}{\text { Flow }} \nonumber \]

The “Pie Wheel” for Detention Time looks like this.

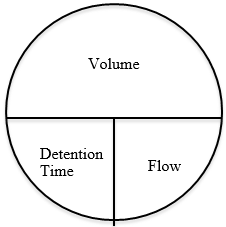
“Units” are extremely important with this formula. There are three variables in this formula; Detention Time, Flow, and Volume. Here are some examples for each.

Detention Time – seconds, minutes, hours, days

Flow – cubic feet per second, gallons per minute, million gallons per day

Volume – cubic feet, gallons, million gallons

Take note at the above examples. If the units are similar (matching) then dividing volume by flow will yield a time (Detention Time). However, simply dividing a volume by a flow will not result in a time. For example, if you divide gallons by cubic feet per second there is no resulting answer. This is because “gallons” and “cubic feet” will not cancel each other.

When solving for Detention Time, the units for Volume and Flow must match. Solving for Detention Time is not the only variable to solve for with this formula. If Detention Time and Volume are given then you will be solving for Flow. Similarly, if Detention Time and Flow are given then you will be solving for Volume. In all of these examples, the units must be similar in order to cancel out and yield your answer.

Using the “unit” examples above, list all possible matches of units in order to cancel and yield an answer.

Volume	Flow	Detention Time

Remember, using the above examples will not provide any answer in HOURS. Always remember to convert your answer to the units specified in the question.

Exercise 9.1

What is the detention time in minutes of a 400,000 gallon sedimentation basin with an average flow rate of 5,000 gpm?An 80 foot tall standpipe is ¾ full. What is the pressure in psi at the bottom?
What is the detention time in hours through a 100,000 gallon reservoir with a flow rate of 750 gpm?A 12” pipeline is flowing water at a velocity of 3.5 fps. What is the corresponding flow rate?
It has been determined that a basin has a detention time of 2 hours and 10 minutes. If the flow through the basin is 2.67 cfs, what is the volume of the basin in gallons?An 18” pipe is flowing 1,500 gpm. What is the velocity?
What is the flow rate (in gpm) through a 40 foot wide, 10 foot deep, 50 foot long basin if the detention time is 1 hour and 55 minutes?ng 4.5 MGD at a velocity of 2.45 fps?
A 25 foot tall reservoir with a 120 foot diameter has a detention time of 3 hours and 22 minutes. What is the daily flow (in MGD) through the reservoir?A 28 foot tall water tank is sitting on a 75 foot tall hill. What is the pressure in a home at the bottom of the hill? (Assume the pressure gauge is 3 feet from the bottom of the home and the tank is full)
A 75 foot long, 30 foot wide, and 20 foot deep basin has a flow of 2.25 MGD. What is the detention time? (Express as hours, minutes, seconds – ex. 5 hours, 3 minutes, and 2 seconds)A home that is receiving water from a water tank that is on top of a 115 foot hill has a pressure of 57 psi. What is the water level in the tank?
A series of tracer studies determined that the detention time through a 2,350,000 gallon basin is 2 hours and 12 minutes. What is the daily flow (in MGD)?
If a flow of 4.45 cfs is moving through 2 miles of 36” diameter pipe, what is the detention time?
A treatment plant has a daily flow of 30 MG. There are two 200,000 gallon sedimentation basins. What is the detention time through the plant.
What is the volume of a reservoir that has a detention time of 29 minutes and a flow of 5.4 cfs?