6.1: It's a Lag in Time

Detention Time is an important process that allows large particles to “settle out” from the flow of water through gravity, prior to filtration. It is the time it takes a particle to travel from one end of a sedimentation basin to the other end. Conventional filtration plants require large areas of land in order to construct sedimentation basins and employ the detention time process. Not all treatment plants have the available land and may decide that direct filtration is suitable. Therefore, in direct filtration plants, the sedimentation process is eliminated. However, in direct filtration plants, the filters have shorter run times and require more frequent backwashing cycles to clean the filters.

A term used that is interchangeable with detention time is contact time. Contact times represent how long a chemical (typically chlorine) is in contact with the water supply prior to delivery to customers. For example, contact time can be measured from the time a well is chlorinated until it reaches the first customer within a community. Or, it could be how long the water mixes in a storage tank before it reaches a customer.

Calculating the Detention Time and Contact Time requires two elements, the volume of the structure holding the water (sedimentation basin, pipeline, and storage tank) and the flow rate of the water (gallons per minute, million gallons per day, etc). Since detention times and contact times are typically expressed in hours, it is important that the correct units are used. When solving Dt problems be sure to convert to the requested unit of time.

As with all water math-related problems, there are other parameters that can be calculated within the problem. For example, if the detention time and volume are known, then the flow rate can be calculated. Or, if the flow rate and detention time are known, the volume can be calculated. Sometimes the flow rate and the desired detention time is known and the size of the vessel holding the water needs to be designed. In this example, the area or dimensions of the structure can be calculated.

Figure \(\PageIndex{1}\)

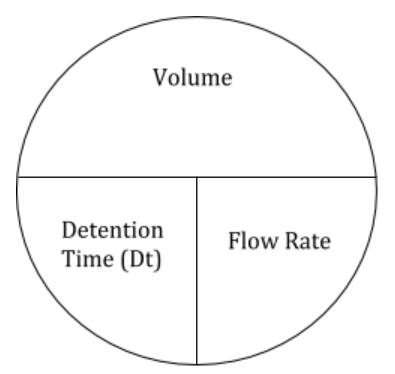
The chart above shows a simple way of calculating the variables. If the variables are next to each other (Dt and Flow Rate) then multiply. If they are over each other (Volume and Dt or Volume and Flow Rate) then divide.

The Detention Time formula is:

\[\text{Detention Time (Dt)} = \dfrac{\text{Volume}}{\text{Flow}}\]

• When solving this equation make sure the units are correct

Take a look at the examples below.

• \(\text{Dt}\) = Volume/Flow
  • gallons/(gallons/minute)
  • cubic feet/(cubic feet/second)
  • gallons/(million gallons/day)

In the first two examples above, the terms can be divided. However, in the third example, they cannot. Dt should be expressed as a unit of time (i.e., sec, min, hours). If you divide the first two examples (gal/gpm and cf/cfs), you will end up with minutes and seconds, respectively. However, in the third example, gallons and million gallons cannot cancel each other out. Therefore, if you had 100,000 gallons as the volume and 1 MGD as the flow rate:

100,000 gallons/1 MGD

Then you would need to convert 1 MGD to 1,000,000 gallons per day in order to cancel the unit gallons. The gallons then cancel leaving “day” as the remaining unit.

100,000 gallons/(1,000,000 gallons/1 day) = 0.1 day

Converting to hours from days is easy, simply multiply by 24 hours per day.

0.1 day/x = 24 hours/1 day = 2.4 hours

Sometimes, this can be the simplest way to solve detention time problems. However, people can be confused when they get an answer such as 0.1 days. There are other ways to solve these problems. One way is to convert MGD to gpm. Using the above example, convert 1 MGD to gpm.

1,000,000 gallons/1 day x 1 day/1,440 minutes = 694.4 gpm

Now solve for the Detention Time.

100,000 gallons/(694.4 gallons/min) = 144 minutes x 1 hour/60 minutes = 2.4 hours

If the question is asking for hours there still needs to be a conversion. However, 144 minutes is more understandable than 0.1 days.

Exercises

Solve the following problems. Be sure you provide the answer in the correct units.

1. What is the detention time in hours of a 100 ft by 20 ft by 10 ft sedimentation basin with a flow of 5 MGD?

2. What is the detention time in a circular clarifier with a depth of 30 ft and a 70 ft diameter if the daily flow is 4.5 MG. (Express your answer in hours:minutes)

3. A water utility engineer is designing a sedimentation basin to treat 10 MGD and maintain a minimum detention time of 2 hours 15 minutes. The basin cannot be longer than 80 feet and wider than 40 feet. Under this scenario, how deep must the basin be?

4. Chlorine is injected into an 18” diameter pipe at a well site. The pipeline is 2,000 ft long before it reaches the first customer. Assuming a well flow rate of 1,700 gpm, what is the detention time (contact time) in minutes?

5. A water utility is designing a transmission pipeline collection system in order to achieve a chlorine contact time of 40 minutes once a 2,250 gpm well is chlorinated. How many feet of 24” diameter pipe are needed?

6. A fluoride tracer study is being conducted at a 15.5 MGD capacity water treatment plant. The contact time through the coagulation and flocculation process is 2.45 hours. If the sedimentation basin has a capacity of 500,000 gallons, what is the total detention time through the 3 processes?

7. The chlorine residual decay rate is 0.2 mg/L per ½ hour in a 5 MG water storage tank. If the storage tank needs to maintain a minimum chlorine residual of 10.0 mg/L what is the required dosage if the tank is filling at a rate of 1,500 gpm until the tank is full?

8. A drinking water well serves a community of 2,000 people. The customer closest to the well is 1,250 feet away. The above-ground portion of the well piping is 12” diameter and 25 feet long. The below-ground portion is 750 feet of 10” diameter and 475 feet of 8” diameter piping. What is the chlorine contact time in minutes from the well head to the first customer? Assume a constant flow rate of 3.90 cfs.

9. An aqueduct has a weir that is 5 feet narrower than the distance across the aqueduct. Assuming a constant weir overflow rate of 28.75 gpm/ft, an average depth of 12 feet, a distance across the bottom of 8 feet, a length of 22 miles, and a daily flow of 0.85 MG, what is the capacity of the aqueduct in AF?

10. A 32-foot tall water storage tank is disinfected with chloramines through an onsite disinfection system. The average constant effluent from the tank is 550 gpm through a 16-inch diameter pipe. If the first customer that receives water from the tank is 3,220 feet from the tank, would the required 45 minute contact time be achieved?

11. A 90-foot diameter, 20-foot deep clarifier maintains a constant weir overflow rate of 15.25 gpm/ft. What is the detention time in hours:min?