6.2: Filtration Rates

Last updated
Save as PDF

Page ID: 7141

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

One of the most important processes in a water treatment plant is filtration. It is the last barrier between the treatment process and the customer. Filters trap or remove particles from the water further reducing the cloudiness or turbidity. There are different shapes, sizes, and types of filters containing one bed or a combination of beds of sand, anthracite coal, or some other form of granular material.

Slow sand filters are the oldest type of municipal water filtration and have filtration rates varying from 0.015 to 0.15 gallons per minute per square foot of filter bed area, depending on the gradation of filter medium and raw water quality. Rapid sand filters, on the other hand, can have filtration rates ranging from 2.0 to 10 gallons per minute per square foot of filter bed area. Typically rapid sand filters will require more frequent backwash cycles to remove the trapped debris from the filters.

Backwashing is the reversal of flow through the filters at a higher rate to remove clogged particles from the filters. Backwash run times can be anywhere from 5–20 minutes with rates ranging from 8 to 25 gallons per minute per square foot of filter bed area, depending on the quality of the pre-filtered water.

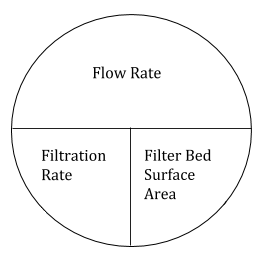
Filtration and backwash rates are calculated by dividing the flow rate through the filter by the surface area of the filter bed. Typically these rates are measured in gallons per minute per square foot of filter bed area.

Flow Rate (gpm)/Surface Area (sq.ft) = Filtration Rate

Although filtration rates are commonly expressed as gpm/ft² they are also expressed as the distance of fall (in inches) within the filter per unit of time (in minutes). During backwashing it is expressed with the same units only per “rise” in the filter. See the example below.

Filtration Rate = Fall (inches)/Time (min)
Backwash Rate = Rise (inches)/Time (min)

Examples

Express 2.5 gpm/ft² as in/min.

First, convert gpm to cfm. The purpose of this is to begin matching the unit of “inches” in in/min to the “cubic feet in cfm.

(2.5 gal/min)/sq.ft x 1 cf/7.48 gal = 0.33 cfm/sq.ft
2.5 gpm/sq.ft x 1 cf/7.48 gal = 0.33 cfm/sq.ft

If you look at the above answer of (0.33 cf/m)/sq.ft more closely you can see that it can also be expressed as 0.33 ft/min since the sq.ft and cf cancel each other to feet.

Once you have “feet per min” you can easily convert to “inches per min” by multiplying by 12.

0.33 ft/min x 12 in/1 ft = 4 in/min

Let’s try another example: What is the filtration rate through a 20’ by 20’ filter if the average flow through the treatment is 2.5 MG?

First, convert 2.5 MGD to gpm. To do this divide 2.5 MGD by 1,440.

2,500,000 gal/day x 1 day/1,440 min = 1,736 gpm

Then divide the flow by the area of the filter (20’ x 20’ = 400 sq.ft).

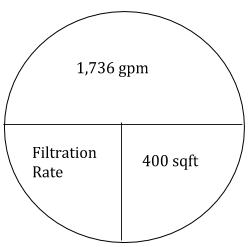
1,736 gpm/400 sq.ft = 4.34 gpm/sq.ft

Now, calculate the inches per minute.

Instead of 7.48 gallons per cubic foot and 12 inches per foot, there is a conversion factor that can also be used.

1.6 in/min = 1 gpm/sq.ft

Exercises

A water treatment plant processes 10.5 MGD. What is the required filter bed area needed to maintain a filtration rate of 1.75 gpm/ft²?
A 15 ft by 17 ft filter needs to be back washed at a rate of 17 gpm/ft² for a minimum of 20 minutes. How many gallons are used during the backwashing process?
In order to properly backwash a certain filter a backwash rate of 20 inches per minute rise is needed. If the filter is 20 ft by 25 ft, what is the backwash flow rate in gpm?
A water treatment plant processes a maximum of 18.65 MGD. The plant has 6 filters measuring 20 ft by 22 ft each. Assuming that each filter receives an equal amount of flow what is the filtration rate in gpm/ft²?
A water treatment plant processes 4.55 MGD through a 35 ft by 35 ft filter. What is the corresponding inches per minute through the filter?
A filter is backwashed at a rate of 15.5 inches per minute for 25 minutes. If the filter is 150 ft², how many gallons were used?
An engineer is designing a circular filter to handle 5.75 MGD and maintain a filtration rate of 1.75 inches per minute. What will the diameter be?
A filter needs to be backwashed when the fall rate exceeds 3.1 inches per minute. It was determined that this rate is reached after 2.3 MG through a 17 ft by 17 ft filter. How often does the filter need backwashing? Give your answer in the most logical time unit.