While many States had standardized testing programs prior to 2000, the number of state-wide tests has grown enormously since then because NCLB required that all states test students in reading and mathematics annually in grades third through eighth and at least once in high school by 2005-6. Twenty-three states expanded their testing programs during 2005-6 and additional tests are being added as testing in science is required by 2007-8. Students with disabilities and English language learners must be included in the testing and provided a variety of accommodations so the majority of staff in school districts are involved in testing in some way (Olson, 2005). In this section we focus on these tests and their implications for teachers and students.
Standards based assessment Academic content standards
NCLB mandates that states must develop academic content standards that specify what students are expected to know or be able to do at each grade level. These content standards used to be called goals and objectives and it is not clear why the labels have changed (Popham, 2004). Content standards are not easy to develop— if they are too broad and not related to grade level, teachers cannot hope to prepare students to meet the standards.
An example, a broad standard in reading is:
"Students should be able to construct meaning through experiences with literature, cultural events and philosophical discussion" (no grade level indicated). (American Federation of Teachers, 2006, p. 6).
Standards that are too narrow can result in a restricted curriculum. An example of a narrow standard might be:
Students can define, compare and contrast, and provide a variety of examples of synonyms and antonyms.
A stronger standard is:
"Students should apply knowledge of word origins, derivations, synonyms, antonyms, and idioms to determine the meaning of words (grade 4) (American Federation of Teachers, 2006, p. 6).
The American Federation of Teachers conducted a study in 2005-6 and reported that some of the standards in reading, math and science were weak in 32 states. States set the strongest standards in science followed by mathematics. Standards in reading were particularly problematic and with one-fifth of all reading standards redundant across the grade levels, i.e. word-by-word repetition across grade levels at least 50 per cent of the time (American Federation of Teachers, 2006).
Even if the standards are strong, there are often so many of them that it is hard for teachers to address them all in a school year. Content standards are developed by curriculum specialists who believe in the importance of their subject area so they tend to develop large numbers of standards for each subject area and grade level. At first glance, it may appear that there are only several broad standards, but under each standard there are subcategories called goals, benchmarks, indicators or objectives (Popham, 2004). For example, Idaho's first grade mathematics standard, judged to be of high quality (AFT 2000) contains five broad standards, including 10 goals and a total of 29 objectives (Idaho Department of Education, 2005-6).
Alignment of standards, testing and classroom curriculum
The state tests must be aligned with strong content standards in order to provide useful feedback about student learning. If there is a mismatch between the academic content standards and the content that is assessed then the test results cannot provide information about students' proficiency on the academic standards. A mismatch not only frustrates the students taking the test, teachers, and administrators it undermines the concept of accountability and the "theory of action" (See box "Deciding for yourself about the research") that underlies the NCLB. Unfortunately, the 2006 Federation of Teachers study indicated that in only 11 states were all the tests aligned with state standards (American Federation of Teachers, 2006).
State standards and their alignment with state assessments should be widely available— preferably posted on the states websites so they can be accessed by school personnel and the public. A number of states have been slow to do this. Table 43 summarizes which states had strong content standards, tests that were aligned with state standards, and adequate documents on online. Only 11 states were judged to meet all three criteria in 2006.
Table \(\PageIndex{1}\) : Strong content standards, alignment, and transparency: evaluation for each state in 2006 (Adapted from American Federation of Teachers, 2006).
| State |
Standards are strong |
Test documents match standards |
Testing documents online |
| Alabama |
|
|
+ |
| Alaska |
|
+ |
+ |
| Arizona |
|
+ |
+ |
| Arkansas |
|
+ |
|
| California |
+ |
+ |
+ |
| Colorado |
|
|
|
| Connecticut |
|
|
|
| Delaware |
|
+ |
|
| District of Columbia |
+ |
+ |
|
| Florida |
|
+ |
+ |
| Georgia |
+ |
|
+ |
| Hawaii |
|
+ |
|
| Idaho |
+ |
|
|
| Illinois |
|
|
+ |
| Indiana |
|
+ |
+ |
| Iowa |
|
+ |
|
| Kansas |
|
+ |
+ |
| Kentucky |
|
+ |
+ |
| Louisiana |
+ |
+ |
+ |
| Maine |
|
+ |
|
| Maryland |
|
+ |
|
| Massachusetts |
+ |
+ |
|
| Michigan |
+ |
+ |
|
| Minnesota |
|
+ |
+ |
| Mississippi |
|
|
+ |
| Missouri |
|
|
|
| Montana |
|
|
|
| Nebraska |
|
|
|
| Nevada |
+ |
+ |
+ |
| New Hampshire |
|
+ |
+ |
| New Jersey |
+ |
|
|
| New Mexico |
+ |
+ |
+ |
| New York |
+ |
+ |
+ |
| North Carolina |
+ |
|
|
| North Dakota |
+ |
+ |
|
| Ohio |
+ |
+ |
+ |
| Oklahoma |
|
+ |
+ |
| Oregon |
|
+ |
+ |
| Pennsylvania |
|
|
+ |
| Rhode Island |
|
+ |
+ |
| South Carolina |
|
|
|
| South Dakota |
+ |
|
+ |
| Tennessee |
+ |
+ |
+ |
| Texas |
|
+ |
+ |
| Utah |
|
|
+ |
Sampling content
When numerous standards have been developed it is impossible for tests to assess all of the standards every year, so the tests sample the content, i.e. measure some but not all the standards every year. Content standards cannot be reliably assessed with only one or two items so the decision to assess one content standard often requires not assessing another. This means if there are too many content standards a significant proportion of them are not measured each year. In this situation, teachers try to guess which content standards will be assessed that year and align their teaching on those specific standards. Of course if these guesses are incorrect students will have studied content not on the test and not studied content that is on the test. Some argue that this is a very serious problem with current state testing and Popham (2004) an expert on testing even said: "What a muddleheaded way to run a testing program." (p. 79)
Adequate Yearly Progress (AYP)
Under NCLB three levels of achievement, basic, proficient and advanced, must be specified for each grade level in each content area by each state. States were required to set a time table from 2002 that insured an increasing percentage of students would reach the proficient levels such that by 2013-14, so every child is performing at or the proficient level. Schools and school districts who meet this timetable are said to meet adequate yearly progress (AYP).
Because every child must reach proficiency by 2013-14 greater increases are required for those schools that had larger percentages of initially lower performing students.
Exhibit \(\PageIndex{1}\) illustrates the progress needed in three hypothetical schools. School A, initially the lowest performing school, has to increase the number of students reaching proficiency by an average of 6 per cent each year, the increase is 3 per cent for School B, and the increase is only 1 per cent for School C. Also, the checkpoint targets in the timetables are determined by the lower performing schools. This is illustrated on the figure by the arrow— it is obvious that School A has to make significant improvements by 2007-8 but School C does not have to improve at all by 2007-8. This means that schools that are initially lower performing are much more likely to fail to make AYP during the initial implementation years of NCLB.
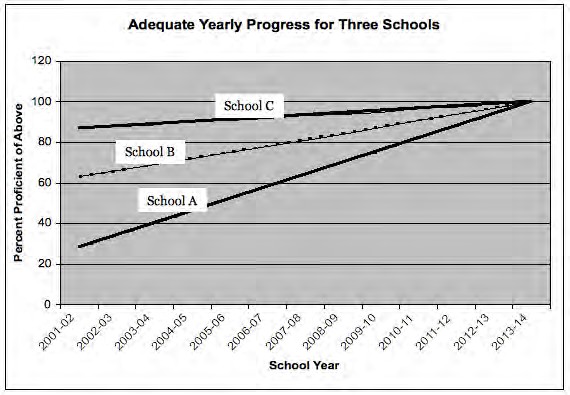
Exhibit \(\PageIndex{1}\): Adequate Yearly Progress requires greater student improvement in schools with lower levels of initial proficiency (CC-BY-NC; K. Siefert, R. Sutton via
Educational Psychology)
Schools A, B and C all must reach 10 per cent student proficiency by 2013-4. However the school that initially has the lowest level of performance (A) has to increase the percentage of students proficient at a greater rate than schools with middle (B) or high (C) levels of initial proficiency rates.
Subgroups
For a school to achieve AYP not only must overall percentages of the students reach proficiency but subgroups must also reach proficiency in a process called desegregation. Prior to NCLB state accountability systems typically focused on overall student performance but this did not provide incentives for schools to focus on the neediest students, e.g. those children living below the poverty line (Hess & Petrilli, 2006). Under NCLB the percentages for each racial/ethnic group in the school (white, African American, Latino, Native American etc.), low income students, students with limited English proficiency, and students with disabilities are all calculated if there are enough students in the subgroup. A school may fail AYP if one group, e.g. English language learners do not make adequate progress. This means that it is more difficult for large diverse schools (typically urban schools) that have many subgroups to meet the demands of AYP than smaller schools with homogeneous student body (Novak & Fuller, 2003). Schools can also fail to make AYP if too few students take the exam. The drafters of the law were concerned that some schools might encourage low-performing students to stay home on the days of testing in order to artificially inflate the scores. So on average at least 95 per cent of any subgroup must take the exams each year or the school may fail to make AYP (Hess & Petrilli, 2006).
Sanctions
Schools failing to meet AYP for consecutive years, experience a series of increasing sanctions. If a school fails to make AYP for two years in row it is labeled "in need of improvement" and school personnel must come up with a school improvement plan that is based on "scientifically based research". In addition, students must be offered the option of transferring to a better performing public school within the district. If the school fails for three consecutive years, free tutoring must be provided to needy students. A fourth year of failure requires "corrective actions" which may include staffing changes, curriculum reforms or extensions of the school day or year. If the school fails to meet AYP for five consecutive years the district must "restructure" which involves major actions such as replacing the majority of the staff, hiring an educational management company, turning the school over to the state.
Growth or value added models
One concern with how AYP is calculated is that it is based on an absolute level of student performance at one point in time and does not measure how much students improve during each year. To illustrate this, Exhibit \(\PageIndex{2}\) shows six students whose science test scores improved from fourth to fifth grade. The circle represents a student's score in fourth grade and the tip of the arrow the test score in fifth grade. Note that students 1, 2, and 3 all reach the level of proficiency (the horizontal dotted line) but students 4, 5 and 6 do not. However, also notice that students 2, 5 and 6 improved much more than students 1, 3, and 4. The current system of AYP rewards students reaching the proficiency level rather than students' growth. This is a particular problem for low performing schools who may be doing an excellent job of improving achievement (students 5 and 6) but do not make the proficiency level. The US Department of Education in 2006 allowed some states to include growth measures into their calculations of AYP. While growth models traditionally tracked the progress of individual students, the term is sometimes used to refer to growth of classes or entire schools (Shaul, 2006).
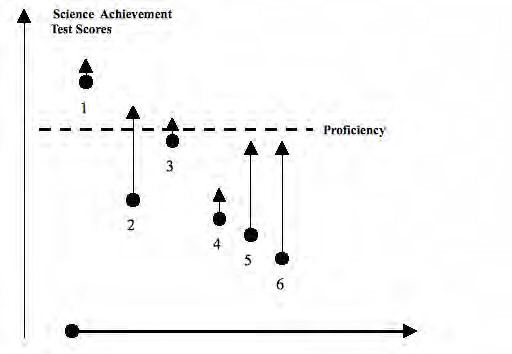
Exhibit \(\PageIndex{2}\): An illustration of value added vs proficiency approach to assessment. Each arrow represents the mathematics achievement results of one student who was tested in the fourth grade (shown by the dot) and also the fifth grade (shown by the tip of the arrow). (CC-BY-NC; K. Siefert, R. Sutton via
Educational Psychology)
Some states include growth information on their report cards. For example, Tennessee ( www.k-12.state.tn.us/rptcrdof; / ) provides details on which schools meet the AYP but also whether the students' scores on tests represent average growth, above average, or below average growth within the state. Exhibit \(\PageIndex{3}\) illustrates in a simple way the kind of information that is provided. Students in schools A, B, and C all reached proficiency and AYP but in Schools D, E, and F did not. However, students in schools A and D had low growth, in schools B and E average growth, in schools C and F high growth. Researchers have found that in some schools students have high levels of achievement but do not grow as much as expected (School A), and also that in some schools, the achievement test scores are not high but the students are growing or learning a lot (School F). These are called "school effects" and represent the effect of the school on the learning of the students.
Exhibit \(\PageIndex{3}\): Proficiency and growth information. (CC-BY-NC; K. Siefert, R. Sutton via Educational Psychology)
| Achievement |
School A |
School B |
School C |
| School D |
School E |
School F |
| Low growth |
Average Growth |
High growth |
| |
Proficiency |
|
Growth over one year
Schools can vary on overall school achievement (proficiency) as well as the amount of growth in student learning, For example schools A, B, and C all have high achievement levels but only in School C do students have, on average, high growth. Schools D, C, and F all have low levels of proficiency but only in school D do students, on average, have low growth.
Growth models have intuitive appeal to teachers as they focus on how much a student learned during the school year— not what the student knew at the start of the school year. The current research evidence suggests that teachers matter a lot— i.e. students learn much more with some teachers than others. For example, in one study low-achieving fourth grade students in Dallas, Texas were followed for three years and 90 per cent of those who had effective teachers passed the seventh grade math test whereas only 42 per cent of those with ineffective teachers passed (cited in Bracey, 2004). Unfortunately, the same study reported that low achieving students were more likely to be assigned to ineffective teachers for three years in a row than high achieving students. Some policy makers believe that teachers who are highly effective should receive rewards including higher salaries or bonuses and that a primary criterion of effectiveness is assessed by growth models, i.e. how much students learn during a year (Hershberg, 2004). However, using growth data to make decisions about teachers is controversial as there is much more statistical uncertainty when using growth measures for a small group or students (e.g. one teacher's students) than larger groups (e.g. all fourth graders in a school district).
Growth models are also used to provide information about the patterns of growth among subgroups of students that may arise from the instructional focus of the teachers. For example, it may be that highest performing students in the classroom gain the most and the lowest performing students gain the least. This suggests that the teacher is focusing on the high achieving students and giving less attention to low achieving students. In contrast, it may be the highest performing students gain the least and the low performing students grow the most suggesting the teacher focuses on the low performing students and paying little attention to the high performing students. If the teacher focuses on the students "in the middle" they may grow the most and the highest and lowest performing students grow the least. Proponents of the value-added or growth models argue that teachers can use this information to help them make informed decisions about their teaching (Hershberg, 2004).
Differing state standards
Under NCLB each state devises their own academic content standards, assessments, and levels of proficiency. Some researchers have suggested that the rules of NCLB have encouraged states to set low levels of proficiency so it is easier to meet AYP each year (Hoff, 2002). Stringency of state levels of proficiency can be examined by comparing state test scores to scores on a national achievement test called the National Assessment of Educational Progress (NAEP). NCLB requires that states administer reading and math NAEP tests to a sample of fourth and eighth grade students every other year. The NAEP is designed to assess the progress of students at the state-wide or national level not individual schools or students and is widely respected as a well designed test that uses current best practices in testing. A large percentage of each test includes constructed-response questions and questions that require the use of calculators and other materials ( http://nces.ed.gov/nationsreportcard ').
Exhibit \(\PageIndex{4}\) illustrates that two states, Colorado and Missouri had very different state performance standards for the fourth grade reading/language arts tests in 2003. On the state assessment 67 per cent of the students in Colorado but only 21 per cent of the students in Missouri were classified as proficient. However, on the NAEP tests 34 per cent of Colorado students and 28 per cent of Missouri students were classified as proficient (Linn 2005). These differences demonstrate that there is no common meaning in current definitions of "proficient achievement" established by the states.
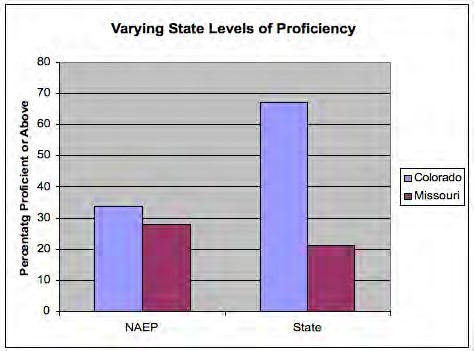
Exhibit \(\PageIndex{4}\): Relationship between state proficiency levels and scores on NAEP (Adapted from Linn 2005).
Implications for beginning teachers
Dr Mucci is the principal of a suburban fourth through sixth grade school in Ohio that continues to meet AYP. We asked her what beginning teachers should know about high stakes testing by the states. "I want beginning teachers to be familiar with the content standards in Ohio because they clearly define what all students should know and be able to do. Not only does teaching revolve around the standards, I only approve requests for materials or professional development if these are related to the standards. I want beginning teachers to understand the concept of data-based decision making. Every year I meet with all the teachers in each grade level (e.g. fourth grade) to look for trends in the previous year's test results and consider remedies based on these trends. I also meet with each teacher in the content areas that are tested and discuss every student's achievement in his or her class so we can develop an instructional plan for every student. All interventions with students are research based. Every teacher in the school is responsible for helping to implement these instructional plans, for example the music or art teachers must incorporate some reading and math into their classes. I also ask all teachers to teach test taking skills, by using similar formats to the state tests, enforcing time limits, making sure students learn to distinguish between questions that required an extended response using complete sentences versus those that only requires one or two words, and ensuring that students answer what is actually being asked. We begin this early in the school year and continue to work on these skills, so by spring, students are familiar with the format, and therefore less anxious about the state test. We do everything possible to set each student up for success."
The impact of testing on classroom teachers does not just occur in Dr Mucci's middle school. A national survey of over 4,000 teachers indicated that the majority of teachers reported that the state mandated tests were compatible with their daily instruction and were based on curriculum frameworks that all teachers should follow. The majority of teachers also reported teaching test taking skills and encouraging students to work hard and prepare. Elementary school teachers reported greater impact of the high stakes tests: 56 per cent reported the tests influenced their teaching daily or a few times a week compared to 46 per cent of middle school teacher and 28 per cent of high school teachers. Even though the teachers had adapted their instruction because of the standardized tests they were skeptical about them with 40 per cent reporting that teachers had found ways to raise test scores without improving student learning and over 70 per cent reporting that the test scores were not an accurate measure of what minority students know and can do (Pedulla, Abrams, Madaus, Russell, Ramos, & Miao; 2003).

 Exhibit \(\PageIndex{2}\): An illustration of value added vs proficiency approach to assessment. Each arrow represents the mathematics achievement results of one student who was tested in the fourth grade (shown by the dot) and also the fifth grade (shown by the tip of the arrow). (CC-BY-NC; K. Siefert, R. Sutton via Educational Psychology)
Exhibit \(\PageIndex{2}\): An illustration of value added vs proficiency approach to assessment. Each arrow represents the mathematics achievement results of one student who was tested in the fourth grade (shown by the dot) and also the fifth grade (shown by the tip of the arrow). (CC-BY-NC; K. Siefert, R. Sutton via Educational Psychology)
 Exhibit \(\PageIndex{4}\): Relationship between state proficiency levels and scores on NAEP (Adapted from Linn 2005).
Exhibit \(\PageIndex{4}\): Relationship between state proficiency levels and scores on NAEP (Adapted from Linn 2005).


