7.7: Leaching
- Page ID
- 44434
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Salinity in the crop root zone can be controlled if the quality of the irrigation water is satisfactory and the flow of water through the soil is sufficient. Leaching, the net downward movement of soil water and solutes, is the key to successful irrigation where salts are a hazard. As the salinity of the irrigation water increases or if more salt sensitive crops are grown, leaching must be increased to maintain high crop yields. This chapter presents general guidelines for leaching that can be applied to various types of irrigation systems; guidelines specific to drip irrigation are presented in Hanson and May (2011). The simplest general expression describing the actual amount of leaching is:
\(L_f=\dfrac{d_p}{d_t}=\dfrac{C_a}{C_d}\) (7.6a)
dt = dz + dr (7.6b)
where: Lf = actual leaching fraction,
dp = depth of water draining below the crop root zone (deep percolation),
dt = total depth of infiltrated water,
Ca = weighted mean salt concentration of the applied water,
Cd = salt concentration of the draining water,
dz = mean depth of infiltrated irrigation, and
dr = depth of infiltrated rainfall.
The weighted mean salt concentration of the applied water can be calculated from:
\(C_a=\dfrac{C_id_z+C_rd_r}{d_z+d_r} \) (7.7)
where: Ci = concentration of irrigation water
Cr = concentration of rain water
The salt concentration of rainfall is so low that it is considered to be zero. Thus, the term Cr dr in Equation 7.7 is zero.
What is the annual leaching fraction of a soil if 300 mm of rain fell during the year, with 250 mm infiltrating into the soil, and 300 mm of irrigation infiltrated? The electrical conductivity of the irrigation water was measured to be 0.5 dS/m at 25° and the electrical conductivity of the soil water draining below the root zone was found to be 2.5 dS/m.
Given: Cd = 2.5 dS/m Ci = 0.5 dS/m
dz = 300 mm dr = 250 mm
Find: The leaching fraction (Lr) for this condition
Solution
\(C_a=\dfrac{C_id_z+C_rd_r}{d_z+d_r} \)
\(C_a = \dfrac{0.5(300)+0(250)}{300+250} \)
\(C_a=0.27\text{ dS/m} \)
\(L_f=\dfrac{C_a}{C_d}=\dfrac{0.27\text{ dS/m}}{2.5\text{ dS/m}} \)
\(L_f=0.11 \)
The leaching requirement (Lr) is the minimum leaching fraction that will prevent a reduction in crop yield. The Lr can be derived from Equation 7.6 as:
\(L_r=\dfrac{d\text{*}_p}{d_t}=\dfrac{C_a}{C\text{*}_d}=\dfrac{EC_a}{EC\text{*}_d} \)
in which the superscript * distinguishes required from actual values. Because electrical conductivity (EC) is easily measured and is almost linearly related to the salt concentration of a relatively dilute salt solution, it is customary to substitute EC for C in these relationships.
Figure 7.11. Graphical solution for the leaching requirement (Lr) as a function of the salinity of the applied water and the salt tolerant threshold value for the crop (adapted from Hoffman and van Genuchten, 1983).
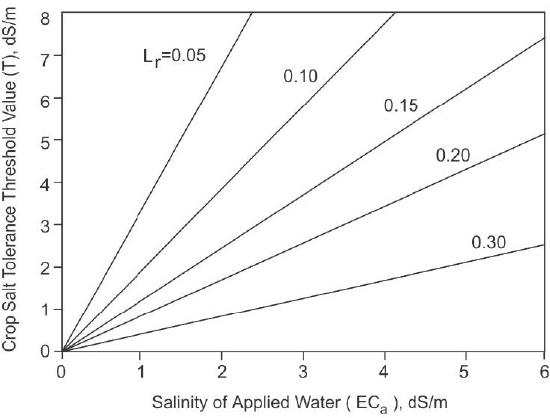
Determine the leaching requirement for tomatoes if the salinity of the irrigation water is 3 dS/m with 16 inches of irrigation water and 4 inches of rainfall contributing to the crop water requirement.
Given: ECi = 3 dS/m
dz = 16 in
dr = 4 in
T for tomatoes is 2.5 dS/m from Table 7.2
Find: Leaching requirement for tomatoes under the specified conditions.
Solution
\(EC_a=\dfrac{EC_i d_z+ EC_r d_r}{d_z + d_r} \)
\(EC_a=\dfrac{3\text{ dS/m }(16\text{ in})+0(4\text{ in})}{16\text{ in}+4\text{ in}} \)
\(EC_a=\dfrac{48}{20}=2.4 \text{ dS/m} \)
From Figure 7.11, for an ECa of 2.4 dS/m and a salt tolerance threshold value of 2.5 dS/m, the leaching requirement is 0.17.
Several mathematical models have been proposed to relate Lr to some readily available value of soil salinity that is indicative of the crop’s leaching requirement. One such model is represented graphically in Figure 7.11. This graphical solution relates the salinity of the applied water, crop salt tolerance threshold, and leaching requirement.
The salt tolerance of many annual crops increases as the growing season progresses. This suggests that if soil salinity levels are low enough at the beginning of the season and adequate amounts of low salt water are applied, soil salinity can be permitted to increase gradually during the irrigation season. For the next crop, rainfall, either singly or in combination with dormant season or pre-plant irrigations, can replenish soil water and leach accumulated salts to permit irrigation the next season without the need for further leaching. An important exception to this procedure is perennial crops, like trees, that form their buds for the next year during the latter half of the irrigation season. High salinity levels during bud formation will be detrimental to fruit production the following season.
If irrigation waters are saline, rainfall and out of season leaching may not be sufficient and leaching during the irrigation season will be required to prevent yield reduction. The key factor to remember is that leaching is not required until accumulated soil salinity surpasses the salt tolerance threshold for the crop. Leaching can be done each irrigation or less frequently, such as seasonally or at even longer periods, provided soil salinity is maintained below the salt tolerance threshold if yield losses are to be avoided.
Some irrigation systems are managed to apply copious amounts of water. Thus, in many cases, this excess amount of irrigation supplies water for leaching without a conscious effort by the irrigator. In some situations, the nonuniform applications of the irrigation system result in some areas of the field receiving water in excess of the crop water and leaching requirements, while underirrigated areas cause water and salt stress. This problem is best solved by an irrigation system that is more uniform in water application rather than applying more water to compensate for nonuniformity.
The leaching requirement model presented here assumes steady state conditions. In reality, steady state never occurs in the field. Several complex computer models have been developed which account for transient conditions that more closely represent field conditions (Minhas et al., 2020). These transient models predict that steady state models overestimate the leaching requirement (Letey et al., 2011; Corwin and Grattan, 2018). Unfortunately, these models require huge data sets, are not readily available to irrigators, and do not directly predict the leaching requirement. Nevertheless, the irrigator should be aware that the leaching requirements given in Figure 7.11 overestimate the amount of saline drainage water entering the environment.

