6.1: Definitions
- Page ID
- 20044
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the Water Industry, often it will be important to calculate perimeter, circumference, area, volume, or surface area (lateral area) of various objects. Let’s start by defining each geometric calculation.
Definitions
Perimeter: The linear measurement or distance around the outside of a two-dimensional object such as a square, rectangle, triangle, etc. The units are expressed as a linear measurement such as inches, feet, yards, miles, millimeters, centimeters, meters, kilometers, etc.
\[P=length\,\, of\,\, side\,\, 1+length\,\, of\,\, side\,\, 2+length\,\, of\,\, side\,\, 3+length\,\, of\,\, side\,\, 4+\dots\]
Circumference: The linear measurement around the outside of a circle. The units are expressed as a linear measurement such as inches, feet, yards, miles, millimeters, centimeters, meters, kilometers, etc. NOTE: Circumference is the name we use to represent the perimeter of a circle.
\[C=\pi (diameter) \,\, \text{or} \,\, C=2\pi (radius)\]
Area (or Surface Area or Lateral Area): The measurement of the amount of space inside a 2-dimensional object or on the surface of a 3-dimensional object. The units are expressed as square linear units such as square inches (in\({}^{2}\)), square meters (m\({}^{2}\)), square feet (ft\({}^{2}\)), etc.
The formula for area depends on the object, so let’s start with the area of some common objects:
| Geometric Measurement | Formula | Shape |
|---|---|---|
| Area of a rectangle | \(A=(length)(width)\) |  |
| Area of a triangle | \(A=\frac{1}{2}(base)(height)\) |  |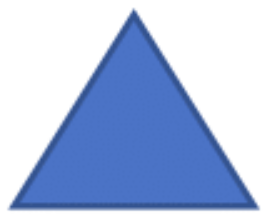
| Area of a circle |
\(A=\pi(radius)^2\) or \( A=(0.785)(diameter)^2 \) |
 |
| Area of a trapezoid | \(A=\frac{1}{2}(base \,\,1+base\,\, 2)(height) \) |  |
Volume: The measurement of the amount of space inside a 3-dimensional object. The units are expressed as cubic linear units such as cubic inches (in\({}^{3}\)), cubic meters (m\({}^{3}\)), cubic feet (ft\({}^{3}\)), etc.
The general formula for volume is: \(Volume=(Area\,\, of\,\, a\,\, surface)(height\,\, or\,\, length)\)
The formula for volume depends on the object, so let’s start with the volume of some common objects:
| Geometric Measurement | Formula | Shape |
|---|---|---|
|
Volume of a Rectangular Box or Prism |
\(V = (length)(width)(height)\) |  |
|
Volume of a Cylinder |
\(V=\pi(radius)^2(height)\) or \(V = (0.785)(diameter)^2(height)\) |
 |
|
Volume of a Cone |
\(V = \frac{1}{3} \pi(radius)^2(height) \) or \(V = \frac{1}{3} (0.785)(diameter)^2(height)\) |
 |
|
Volume of a Sphere |
\(V = \frac{4}{3} \pi(radius)^3\) or \(V=\frac{2}{3}(0.785)(diameter)^3\) |
 |
|
Volume of a Triangular Prism |
\(V=(Area\,\, of\,\, the\,\, triangular\,\, surface)(depth)\) or \(V=\frac{1}{2} (base)(height)(depth \,\, or \,\, width)\) |
 |
|
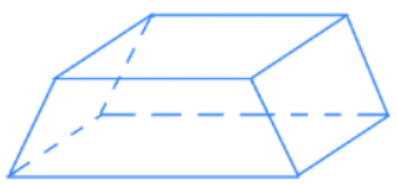
Volume of a Trapezoidal Prism |
\(V = (Area \,\, of\,\, the \,\, trapezoidal \,\, surface)(depth)\) or \(V=\frac{1}{2}(base \,\, 1+base\,\, 2)(height)(depth \,\, or\,\, width) \) |
 |