Skip to main content
Workforce LibreTexts

6.2: Examples

  1. Last updated
  2. Save as PDF
  • Page ID
    20045

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
    1. Calculate the perimeter (or circumference if appropriate) and area of the following shapes:
      1. Calculate the perimeter and area of the rectangle using the figure below.

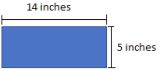
    clipboard_eafcdea686f8b83a164cbb09484ca6b70.png

    \(\begin{aligned} \text{Perimeter} &= \text{sum of the lengths of the sides}\\ &= \text{14 in+5 in+14 in+5 in=2(14 in)+2(5 in)} \\ &= \text{ 28 in+10 in=38 in}\end{aligned}\)

    Area = (length)*(width) = \(\left(14\,\, in\right)\left(5\,\, in\right)=70\,\, in^2\)

    1. Calculate the circumference and area of the circle using the figure below.

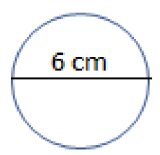
    clipboard_ec875222934ed71ef4b5bca68738f038b.png

    Circumference = \(\pi \left(diameter\right)=\pi \left(6\,\, cm\right)=\left(3.14\right)\left(6\,\, cm\right)=18.84\,\, cm\)

    Area = \(\left(0.785\right){\left(diameter\right)}^2=\left(0.785\right){\left(6\,\, cm\right)}^2=\left(0.785\right)\left(36\,\, cm^2\right)=28.26\ cm^2\)

    1. Calculate the area of the figures below.
      1. A triangle with height of 7 meters and a base of 15 meters.

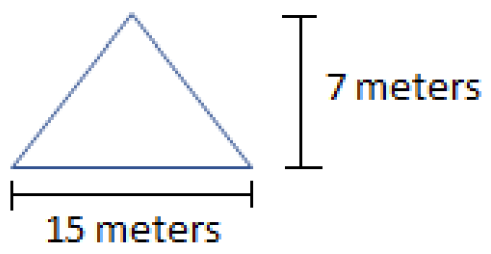
    clipboard_eddb1017f00ea012f0610e86bc1c7072b.png

    Area = \(\frac{1}{2}\left(base\right)\left(height\right)=\frac{1}{2}\left(15\,\, m\right)\left(7\,\, m\right)=\frac{1}{2}\left(105\,\, m^2\right)=52.5\,\, m^2\)

    1. A trapezoid with a height of 5 feet and bases of 3 feet and 10 feet.

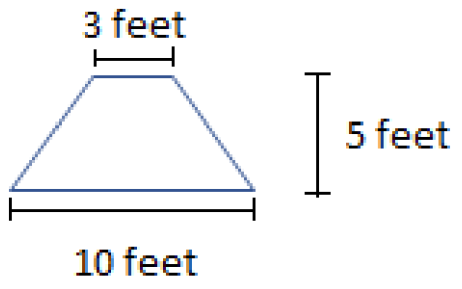
    clipboard_eec8892f4f9a1144e90dd070ea39ca2d2.png

    \(\begin{aligned}\text{Area} &= \frac{1}{2}(base\,\, 1+base\,\, 2)(height) \\ &= \frac{1}{2} (3\,\, ft+10\,\, ft)(5\,\, ft) \\ &= \frac{1}{2}(13\,\, ft)(5\,\, ft) \\ &= \frac{1}{2} \left(65\,\, ft^2\right)=32.5\,\, ft^2 \end{aligned} \)

    1. Calculate the perimeter and area of the following figure

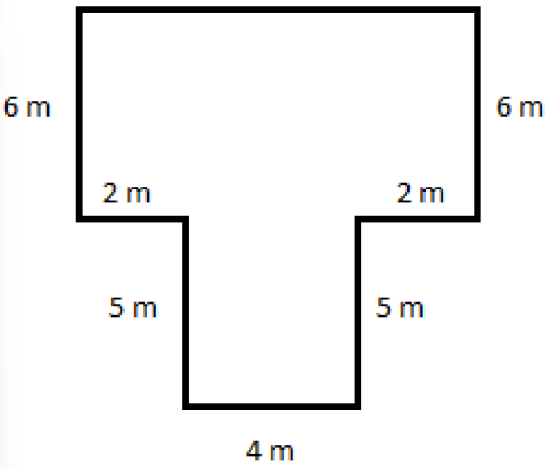
    clipboard_ef8097a296d8e904e7d812c8c0b4c76e1.png

    1. Calculate the perimeter.

    Since the perimeter is the distance around the outer edges, we can calculate the distance across the top edge to be the sum of the lower horizontal edges, namely \(2\,\, m\,\, +\,\, 4\,\, m\,\, +\,\, 2\,\, m\,\, =\,\, 8\,\, m\)

    Next, add the lengths of the outer edges to obtain

    \(\begin{aligned} \text{Perimeter} &=8\,\, m+6\,\, m+2\,\, m+5\,\, m+4\,\, m+5\,\, m+2\,\, m+6\,\, m \\ &= 8\,\, m+2\left(6\,\, m\right)+2\left(2\,\, m\right)+2 \left(5\,\, m\right)+4\,\, m \\ &=8\,\, m+12\,\, m+4\,\, m+10\,\, m+4\,\, m\\ &=38\,\, m\end{aligned}\)

    1. Calculate the area.

    Using a dashed line, divide the figure into two rectangles by drawing a horizontal line through the figure at the 2 m markings

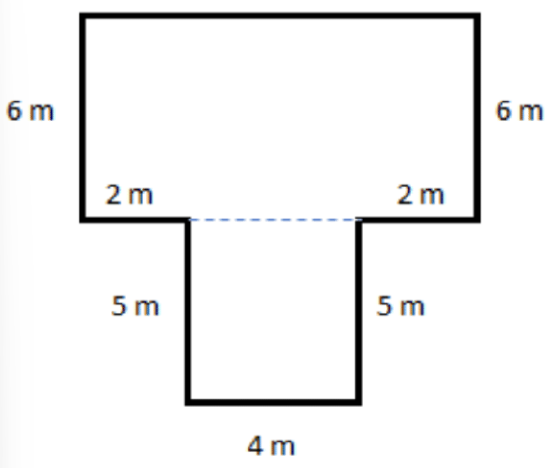
    clipboard_e03f2badf807e268b6dfc5684dec6f162.png

    Next, find the area of each figure and add the results to obtain the area of the original figure.

    The area of the upper rectangle = A\({}_{1}\) = \(\left(6\,\, m\right)\left(8\,\, m\right)=48\,\, m^2\)

    The area of the lower rectangle = A\({}_{2}\) = \(\left(5\,\, m\right)\left(4\,\, m\right)=20\,\, m^2\)

    Total Area = A\({}_{1}\) + A\({}_{2}\) = \(48\,\, m^2+20\,\, m^2=68\,\, m^2\)

    1. Calculate the perimeter and area of the figure below.

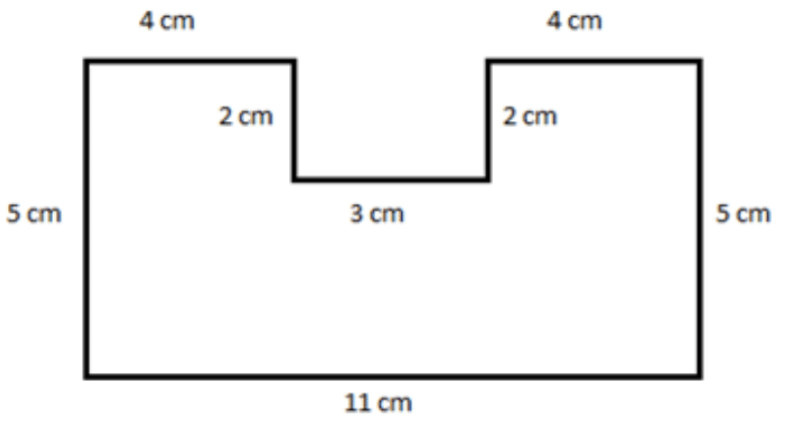
    clipboard_e3a0bc98baf654a531cca1adadd9d34c4.png

    1. Calculate the perimeter.

    Since the perimeter is the distance around the outer edges, we add the lengths of the edges to obtain

    \(\begin{aligned}\text{Perimeter} &= 4\,\, cm+2\,\, cm+3\,\, cm+2\,\, cm+4\,\, cm+5\,\, cm+11\,\, cm+5\,\, cm \\ &= 2\left(4\,\, cm\right)+2\left(2\,\, cm\right)+3\,\, cm+2\left(5\,\, cm\right)+11\,\, cm \\ &= 8\,\, cm+4\,\, cm+3\,\, cm+10\,\, cm+11\,\, cm\\ &=36\,\, cm\end{aligned} \)

    1. Calculate the area.

    We can compute the area of this figure in one of two ways, either using addition or by using subtraction. Let’s investigate both methods.

    1. Using Addition

    Divide the figure into three rectangles by drawing a dashed line from the left side of the figure through to the right side of the figure, connecting at the 3 cm line.

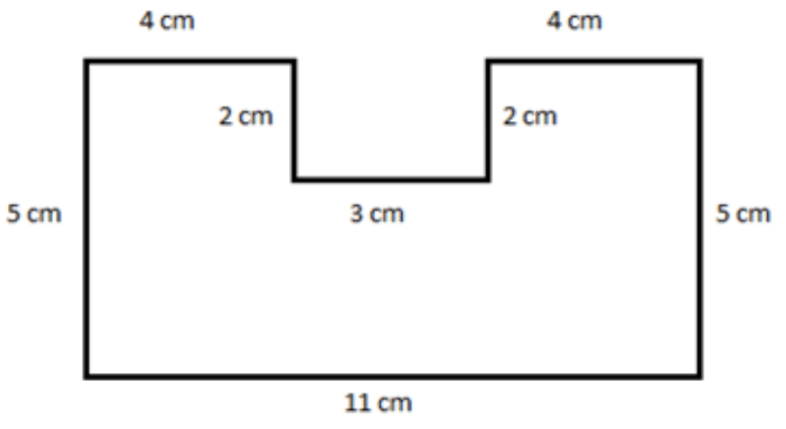
    clipboard_ebc9daa9f14fcf08ad2715aade5b659fa.png

    Calculate the area of each rectangle and add the results; let’s notice that the two upper rectangles are the same size

    Area of small rectangle \(=\left(4\,\, cm\right)\left(2\,\, cm\right)=8\,\, cm^2\)

    Area of large rectangle \(=\left(3\,\, cm\right)\left(11\,\, cm\right)=33\,\, cm^2\)

    Total area \(=8\,\, cm^2+8\,\, cm^2+33\,\, cm^2=49\,\, cm^2\)

    1. Using Subtraction

    Find the area of the outer rectangle and subtract the area of the rectangular hole, so now let’s draw a horizontal dashed line across the top opening of the figure

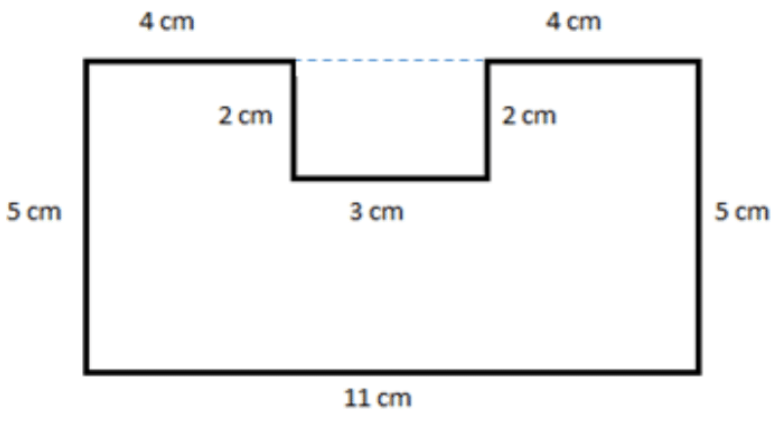
    clipboard_eea981cf307c69a5efb5e2038ccae8e82.png

    Next, let’s find the area of the larger outer edge rectangle

    Area of large rectangle \(=\left(5\,\, cm\right)\left(11\,\, cm\right)=55\,\, cm^2\)

    Area of the rectangular hole \(=\left(2\,\, cm\right)\left(3\,\, cm\right)=6\,\, cm^2\)

    \(\begin{aligned} \text{Total Area} &= \text{Area of large outer rectangle – Area of the rectangular hole} \\ &=55\,\, cm^2-6\,\, cm^2=49\,\, cm^2\end{aligned} \)

    1. A rectangular pool measures 28 feet by 52 feet. Surrounding (and bordering) the basin is a path 3 feet wide. Find the area of the path.

    First, let’s draw a figure to depict the scenario. Let’s start by drawing a rectangle to represent the pool.

    clipboard_ea49c2d18351ff38a6bdabd16cbd19e1b.png

    Next, let’s draw the 3 ft wide border around the pool to represent the path. The path is represented by the shaded region.

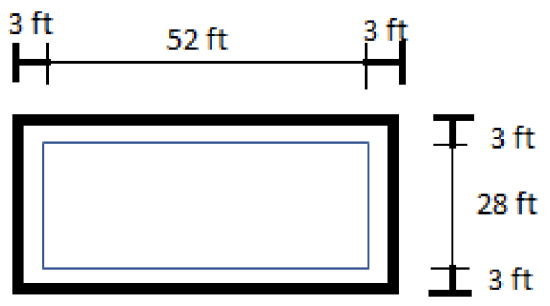
    clipboard_eda71fc97aabb35d0f5c7ac36c975b7ad.png

    The outer edge of the path creates a larger rectangle whose length is the length of the pool plus twice the width of the path or 52 ft + 2(3 ft) = 58 ft. The width of the outer edge of the path is the width of the pool plus twice the width of the path or 28 ft + 2(3 ft) = 34 ft.

    To obtain the area of the path, find

    the area of the outer edge - the area enclosed by the pool = area of the path

    \(\begin{aligned} \text{Area of the path} &= \left(58\,\, ft\right)\left(34\,\, ft\right)-(28\,\, ft)(52\,\, ft) \\ &=1972\,\, ft^2-1456\,\, ft^2\\ &=516\,\, ft^2 \end{aligned} \)

    1. Calculate the lateral area (surface area) of a triangular prism as shown below

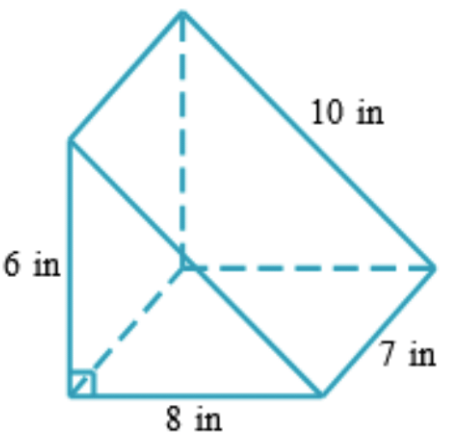
    clipboard_e2cd5180a63bedd199b897992db7a595f.png

    There are five sides or surfaces to this triangular prism. Two of the sides are triangles of the same size, namely with a height of 6 inches and a base of 8 inches and the other three sides are rectangles, the left face is 6 inches by 7 inches rectangle, the bottom face is 8 inches by 7 inches rectangle, and the right-side face is 10 inches by 7 inches rectangle.

    To calculate the lateral area or surface area, we find the area of all the surfaces and add the results

    Area of the two triangles \(=2\left[\frac{1}{2}\left(8\,\, in\right)\left(6\,\, in\right)\right]=48\,\, in^2\)

    \(\begin{aligned}\text{Area of the three rectangles} &=\left(6\,\, in\right)\left(7\,\, in\right)+\left(8\,\, in\right)\left(7\,\, in\right)+\left(10\,\, in\right)\left(7\,\, in\right) \\ &=42\,\, in^2+56\,\, in^2+70\,\, in^2\\ &=168\,\, in^2\end{aligned} \)

    Lateral area \(=48\,\, in^2+168\,\, in^2=216\,\, in^2\)

    More examples using volume of three-dimensional objects

    1. Calculate the volume of the rectangular prism with dimensions 2 yds X 6 yds X 7 yds.

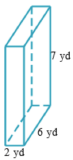
    clipboard_ea4965ce5eff5a1081fcbff7d1dd1fada.png

    \[Volume=\left(length\right)\left(width\right)\left(height\right)=\left(2\,\, yds\right)\left(6\,\, yds\right)\left(7\,\, yds\right)=84\,\, yds^3\nonumber \]

    1. Calculate the volume of a triangular prism as shown below.

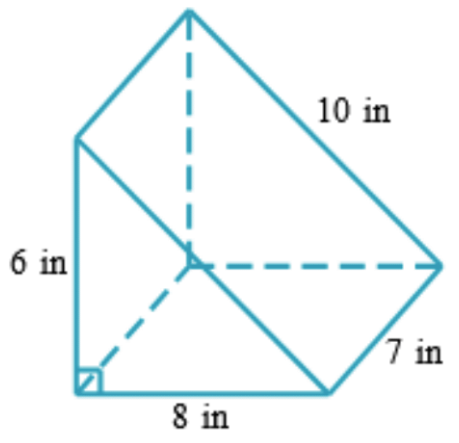
    clipboard_e66ecf892ab7cb65e8a5f979185b71b4a.png

    \[V=\frac{1}{2}\left(base\right)\left(height\right)\left(depth\,\, or\,\, width\right) \nonumber \]

    \[V=\frac{1}{2}\left(8\,\, in\right)\left(6\,\, in\right)\left(7\,\, in\right)=168\,\, in^3 \nonumber \]

    1. Calculate the volume of a sphere with a diameter of 15.6 mm.

    \[V=\frac{2}{3}\left(0.785\right){\left(diameter\right)}^3=\frac{2}{3}\left(0.785\right){\left(15.6\,\, mm\right)}^3=\frac{2}{3}\left(0.785\right)\left(3796.416\,\, mm^3\right)=1986.8\,\, mm^3 \nonumber \]

    1. Calculate the volume of the object below (not drawn to scale)

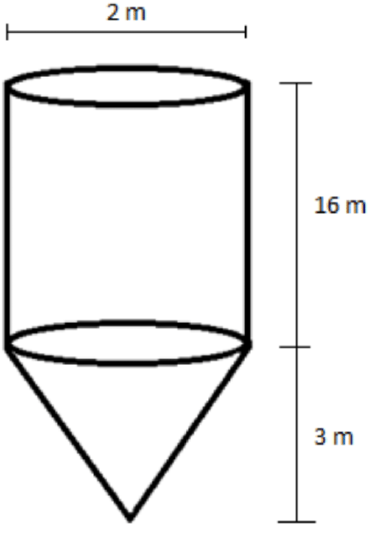
    clipboard_e07d9895431c87aa5005dc6cf4e0f0207.png

    \[\begin{aligned} \text{Total Volume} &=\text{Volume of the cylinder + Volume of the cone} \\ \text{Volume of cylinder} &=\left(0.785\right){\left(diameter\right)}^2\left(height\right) \\ &=\left(0.785\right){\left(2\,\, m\right)}^2\left(16\,\, m\right) \\ &= \left(0.785\right)\left(4\,\, m^2\right)\left(16\,\, m\right) \\ &=\left(0.785\right)\left(64\,\, m^3\right)\\ &=50.24\,\, m^3\end{aligned}\]

    \[\begin{aligned} \text{Volume of cone} &=\frac{1}{3}(0.785)\left(diameter\right)^2\left(height\right) \\ &= \frac{1}{3}\left(0.785\right)\left(2\,\, m\right)^2\left(3\,\, m\right)\\ &= \frac{1}{3} \left(0.785\right)\left(4\,\, m^2\right)\left(3\,\, m\right)\\ &=\frac{1}{3} \left(0.785\right)\left(12\,\, m^3\right)\\ &=3.14\,\, m^3\end{aligned} \]

    \[\begin{aligned} \text{Total Volume} &= \text{Volume of the cylinder + Volume of the cone}\\ &=50.24\,\, m^3+3.14\,\, m^3 \\ &=53.38\,\, m^3 \end{aligned} \]

    This page titled 6.2: Examples is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Kelly Brooks.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      Kelly Brooks
      License
      CC BY
      License Version
      4.0
      Show TOC
      no
    2. Tags
      This page has no tags.