1.4: Multiplying Fractions
- Page ID
- 7084
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Multiplying and dividing fractions is a common practice when solving water related math problems. However, the process may not appear to be the multiplication and division of fractions and is commonly referred to as “unit conversion” or unit dimensional analysis. The example below demonstrates this process and will be discussed in more detail later in this text.
\[\dfrac{2 \text{sqft}}{1} \times \dfrac{3 \text{ft}}{1 \text{sec}}=\dfrac{6 \text{cf}}{\text{sec} } \nonumber \]
For now, ignore the “units” and focus on solving the math. “Unit Dimensional Analysis” is a section we will spend a significant amount of time covering. Just look at the above problem as a fraction multiplication problem. Yes, both 2 over 1 and 3 over 1 are simply 2 and 3, but it helps to illustrate the process by looking at them as fractions.
\[\dfrac{2}{1} \times \dfrac{3}{1}=\dfrac{6}{1} \nonumber \]
When multiplying fractions the numerators are multiplied by each other and the denominators are multiplied by each other. In other words, the numbers are multiplied straight across. So, in the example above, 2 x 3 = 6 and 1 x 1 = 1. The resulting answer is 6 over 1 or more simply put 6. However, when “units” are introduced, you can’t just say the answer is “6”. Always remember to reduce as necessary. Look at a couple other examples below:
Example \(\PageIndex{1}\)
\(\dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{1}{4}\)
Example \(\PageIndex{2}\)
\(\dfrac{2}{3} \times \dfrac{4}{6}=\dfrac{8}{18} \div \dfrac{2}{2}=\dfrac{4}{9}\)
In the first Example \(\PageIndex{1}\), if you multiply the numbers across as before, you would multiply 1 times 1 and then 2 x 2. The resulting answer would be 1 over 4 or one forth. In the next Example \(\PageIndex{2}\) you can do the same thing. Multiply the 2 and 4 to get 8 and then multiply the 3 and 6 to get 18. The resulting answer is 8 over 18 or eight eighteenths. However, remember to always reduce if necessary. In order to reduce you need to find a number, which will go into both 8 and 18. Since 2 will go into both of these numbers, you can reduce the answer to 4 over 9 or four ninths.
Cross canceling is also something you can do. Cross canceling is nothing more than reducing before you multiply. Look for any number that goes into both a numerator and a denominator. In the example below, 2 goes into both the 2 in the first fraction and the 6 in the second fraction.
Example \(\PageIndex{3}\)
\(\dfrac{2}{3} \times \dfrac{4}{6}=\dfrac{\not{2}}{3} \times \dfrac{4}{\not{6}}=\dfrac{1}{3} \times \dfrac{4}{3}=\dfrac{4}{9}\)
In the Example \(\PageIndex{3}\), when you cross cancel, you reduce the two-thirds times four sixths to one third times four thirds. Then you multiply the 1 and 4 (numerators) and the 3 times 3 (denominators) to get an answer of four ninths.
When multiplying whole numbers and fractions you must first convert the whole number into an improper fraction and then, multiply. Be sure to cross cancel if possible and reduce if necessary. Placing a whole number over a 1 is an important step not only in solving these types of fraction problems, but will also be a helpful tool later in this text.
Example \(\PageIndex{4}\)
\(5 \times \dfrac{3}{5}=\dfrac{5}{1} \times \dfrac{3}{5} \rightarrow \dfrac{\not{5}}{1} \times \dfrac{3}{\not{5}}=\dfrac{3}{1}=3\)
The same rules apply when multiplying mixed numbers. Convert to improper fractions and multiply. In order to convert mixed numbers into improper fractions you must multiply the denominator by the whole number. Then add the numerator to the product and put that number over the denominator. Be sure to cross cancel if possible and reduce if necessary. Note: Never leave an answer as an improper fraction.
Example \(\PageIndex{5}\)
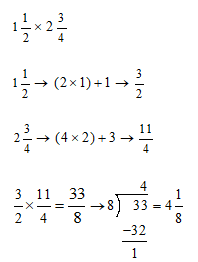
Exercise 1.4
Multiply the following and reduce if necessary. Remember to cross cancel if possible. If you are multiplying a whole number by a fraction, place the whole number over 1.
- \(\dfrac{1}{2} \times \dfrac{2}{4}\)
- \(8 \times 3 \dfrac{2}{5}\)
- \(\dfrac{18}{4} \times \dfrac{12}{9}\)
- \(1 \dfrac{10}{9} \times 4 \dfrac{4}{7}\)
- \(5 \dfrac{9}{3} \times 7 \dfrac{3}{5}\)
- \(\dfrac{21}{24} \times \dfrac{4}{7} \times \dfrac{6}{3}\)
- \(\dfrac{1}{100} \times \dfrac{10}{20}\)
- \(\dfrac{13}{33} \times \dfrac{13}{33}\)
- \(10 \dfrac{12}{15} \times 10 \dfrac{12}{15}\)
- \(8 \dfrac{1}{3} \times 5 \dfrac{3}{5}\)
- \(\dfrac{3}{4} \times \dfrac{6}{9} \times \dfrac{10}{12} \times \dfrac{12}{20}\)
- \(\dfrac{100}{200} \times \dfrac{10}{20}\)
- \(\dfrac{4}{5} \times \dfrac{5}{4}\)
- \(15 \times 7 \dfrac{1}{5}\)

