9.3: Filtration Rate
- Page ID
- 7104
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Filtration is the last stage in the treatment process for removing particles from the water. The filtration media can vary from sand to gravel to anthracite coal to garnet or a variety of materials layered to trap the remaining suspended solids in the water. Filtration rate is the measure of how much water passes through a certain sized filter over a specific time. Typically filtration rates are expressed in gallons per minute per square foot of filter area (gpm/ft\(^2\)). It is the flow of water through the surface area of a filter.
In the picture below a filter is 5 ft by 5 ft and divided into 1 ft by 1 ft sections. This is done to demonstrate how filtration rates are expressed (in 1 ft\(^2\) sections).
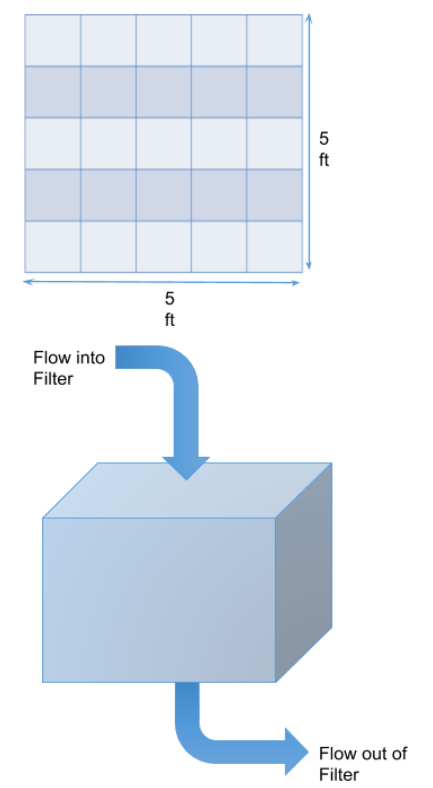
As flow enters a filter it travels down through the media and then out to either a finished water clear well for distribution or perhaps disinfected prior to delivery.
This is the formula used for Filtration Rates:
\[\mathrm{FR}=\dfrac{\text { Flow }}{\text { SurfaceArea }} \nonumber \]
Since Filtration Rates are expressed as gpm/ft\(^2\) then it only makes sense to convert the flow rate to gpm prior to dividing by the filter surface area. However, in this equation it is not necessary to do so prior to dividing.
The “Pie-Wheel” for Filtration Rates looks like this:
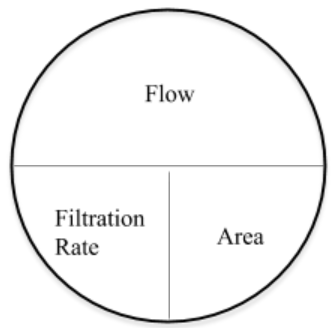
Remember that the units for the flow and area will determine the unit for filtration rate.
Example \(\PageIndex{1}\)
A water treatment plant with a 100 ft2 filter has a flow of 1,650 gpm. What is the filtration rate expressed in gpm/ft\(^2\).
Solution
\[\dfrac{1,650 \mathrm{gpm}}{100 \mathrm{ft}^{2}}=16.5 \mathrm{gpm} / \mathrm{ft}^{2} \nonumber \]
This is a straight forward example with the units given in the same units requested to be expressed in the answer. Let’s try another.
Example \(\PageIndex{2}\)
A water treatment plant has an average daily flow of 10.5 MGD. The filter at the end of the treatment process is 22 ft by 15 ft. What is the filtration rate expressed as gpm/ft\(^2\)?
Solution
In this question you need to calculate the area of the filter and determine if you want to convert the daily flow to gpm before or after you divide it by the area. Both ways of solving are explained below.
\[\dfrac{10.5 \mathrm{MGD}}{22 \mathrm{ft} \times 15 \mathrm{ft}}=\dfrac{10.5 \mathrm{MGD}}{330 \mathrm{ft}^{2}}=0.032 \mathrm{MGD} / \mathrm{ft}^{2} \nonumber \]
Note that the units are million gallons per day per square feet and need to be converted to gpm/ft\(^2\).
\[\dfrac{0.032 \mathrm{MG}}{\text { Day }}=\dfrac{32,000 \mathrm{gal}}{\text { Day }} \times \dfrac{1 \text { day }}{24 \text { hours }} \times \dfrac{1 \text { hour }}{60 \mathrm{min}}=22.2 \mathrm{gpm} / \mathrm{ft}^{2} \nonumber \]
Another way to solve this is to convert the flow to gpm before you divide it by the area.
\[\dfrac{10,500,000 \text { gal }}{\text { day }} \times \frac{1 \text { day }}{24 \text { hours }} \times \frac{1 \text { hour }}{60 \text { min }}=\frac{7,291.7 \text { gallons }}{\text { minute }} \nonumber \]
Then plug this into the filtration rate formula.
\[\dfrac{7,292 \text { gal }}{22 \mathrm{ft} \times 15 \mathrm{ft}}=\dfrac{7,291 \mathrm{gal}}{330 \mathrm{ft}^{2}}=22.1 \mathrm{gpm} / \mathrm{ft}^{2} \nonumber \]
Take note that the answers are slightly different (0.1 off.) This is only due to rounding. If both solutions for this problem are rounded to the same number of digits you would get the exact same answer.
Exercise 9.3
(Express all filtration rates as gpm/ft\(^2\))
- A water treatment plant has a typical flow through a 175 ft\(^2\) filter of 755 gpm. What is the filtration rate?
- A circular filter with a diameter of 74 feet receives a flow of 2,200 gpm. What is the filtration rate?
- A three-hour test revealed that 75,000 gallons passed through a filter with dimensions of 10 ft by 20 ft. Find the filtration rate.
- A water treatment plant has a total of 4 filters. The plant is designed to treat a daily flow of 7.25 million gallons. The target filtration rate is 2.25 gpm/ft\(^2\). Assuming that all 4 filters are identical in size, what is the area of each filter?
- What is the rated capacity in MGD of a rapid sand filter that is 25 ft long and 16 feet wide when operated at a filtration rate of 1.75 gpm/ft\(^2\)?
- It was determined that the optimum filtration rate of a filter with the dimensions of 12 ft wide and 18 feet long is 2.45 gpm/ft\(^2\). What is the maximum flow rate in cfs?
- A water treatment plant treated 70 million gallons through 3 identical filters in one week. If the average filtration rate was 3.15 gpm/ft\(^2\), what is the area of each filter?
Periodically, filters will need to be cleaned. Cleaning is done through a routine process called backwash. As filters remove particles, the efficiency decreases and the flow rates slow. At predetermined intervals, treatment operators will backwash the filters. Backwashing is nothing more than reversing the flows. However, backwashing rates are typically 10 or more times greater than filtration rates.
- After 6 hours in operation a 20ft by 30 ft filter required backwashing. Assuming a flow rate of 10,000 gpm, what was the backwash rate?
- A 15 ft by 17 ft filter was backwashed at a rate of 22.5 gpm/ft\(^2\) for 20 minutes. How many gallons were used for the backwashing process?
- It was determined that a filter with a surface area of 725 ft\(^2\) needs to be backwashed for 12 minutes using 94,500 gallons. What would the corresponding backwash rate be in gpm/ft\(^2\)?

