6.2: Appendix II- Parameterization
- Page ID
- 23008
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What is parameterization
To understand what parameterization is and how it works, let us consider a simple, basic example: the equation that describes a straight line:
y = a·x + b
In this equation, x and y are the coordinates of each point on the line, and a and b are parameters. The values of these parameters do not change the line type: the equation always describes a straight line. What a and b do is determine key properties of the line:
- a determines the slope of the line: if it is negative, the line goes down to the left; if it is positive, down to the right; if its is 1, the slope is 45 degrees; if it is zero, the line is horizontal
- b determines the y intercept: the point where the line crosses the y axis

Instead of fixed values, the two parameters can be variable, so that we can control them in a transparent and precise manner. Moving a line to a new position without changing its slope, for instance, amounts to adding a number to b. Parameter values can be constrained to take specific values, e.g. if a can only be -1 or +1, the equation is allowed to produce only line slopes of 45 degrees. They can also be constrained relative to parameters of other lines. For example, this equation describes lines that are always parallel to our original example:
y1 = a·x1 + (b + c)
The following equation describes lines that are always perpendicular to our example:
y2 = (-1/a)·x2 + (b + d)
Any change to the parameters of the original line also triggers changes to the other two lines, so that they always remain respectively parallel and perpendicular to it. Constraining one thing relative to another in this way is the foundation of parameterization in design, for example, keeping walls parallel or perpendicular to each other, keeping their dimensions in the same proportions etc.
Kinds of parameterization
There are three kinds of parameterization in design:
- Geometric: affecting the geometric properties of a symbol, e.g. length or slope
- Topological: concerning the number and configuration of symbols, e.g. the number and position of steps in a stair in relation to the height that has to be bridged
- Symbolic: concerning non-geometric properties of a symbol, e.g. the type of a wall one may enter in a model can be constrained by applicable fire safety regulations or acoustic requirements
The above line example is of the geometric kind. Figure 2 is an example of the topological kind: a helical stair, consisting of geometrically identical steps. Each step is positioned with the bottom line of its riser fully aligned with the far end of the tread of the previous step. In this way, there are no gaps between them and they form a steady progression from a lower level to a higher.
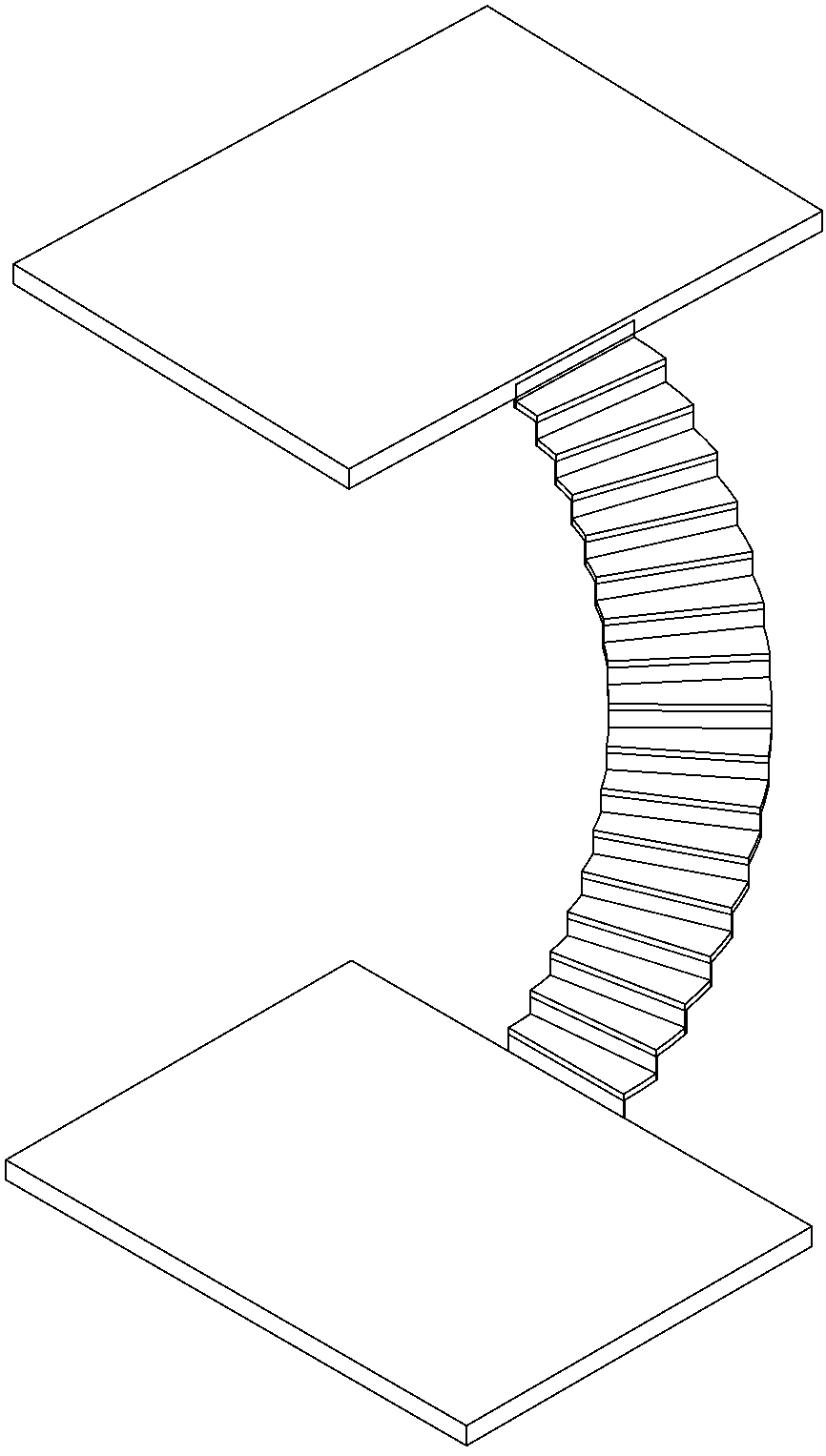
If the height difference between the two floors changes (Figure 3 and 4), more steps are added in the same fashion: topological parameterization affects the number of required steps. The geometry of the steps and their relation do not change, in contrast to the overall form of the stair.


One can also choose to modify the geometry of the steps when the height difference between floors changes: keep the number of steps the same and increase or decrease the rise of each step. In this case, which is possible only with small height differences that do not destroy the climbability of the stair, the parameterization is geometric.
Symbolic parameterization concerns non-geometric values, which can nevertheless be fundamentally quantitative. For example, around a music room in a school one needs to have walls and floors with a heavier acoustic insulation than in other parts of the building, while the walls and floors around a chemistry lab must have a higher fire resistance: the use of the space imposes a threshold of acceptable acoustic or fire-resistance performance. Each type of wall and floor in BIM can be automatically evaluated against this threshold, resulting in automatic warnings or even refusal when an inappropriate symbol is entered in the model. The values that are compared in this example are numerical (the threshold required by the space versus the relevant performance of the wall) but the parametric relation is between space use type and wall or floor type. Similarly, the colour design of a space can be based on a monochromatic scheme with variations in lightness and saturation. If the primary colour in the scheme changes, then all these variations are adapted, resulting in different RAL or Pantone codes.
Parameterization and semantic data types
One of the interesting effects of parameterization is on the semantic type of symbol properties: it turns primary data into derivative. The length of a wall is normally primary information because it is an essential part of its identity. However, if a particular wall is constrained to have the same length as another wall, then the length of the former becomes derivative, as it follows any change to the length of the latter. Removing the constraint makes the two walls independent of each other and makes the length of both primary again.
This example illustrates the significance and complexity of parameterization in design: on one hand, parameterization makes the configuration and modification of a symbolic representation easier and safer. Rather than having to adjust the dimensions of every wall separately, we can relate them all to each other, establishing a parametric network that supports the propagation of changes to one wall to all others. Unfortunately, such a network is had to define because we have to anticipate all possible changes to every wall and their significance to others. Relating everything to a single wall and then manipulating only than one is practically never the answer.
Moreover, each symbol in the representation may belong to multiple networks. A wall, for example, can be related to geometric parametric networks that affect its dimensions; to acoustic parametric networks that constrain properties relevant to acoustics, such as mass and rigidity, relative to the activities taking place on either side of the wall; to fire safety parametric networks that constrain other material properties relative to the location of the wall along egress routes or fire compartment boundaries. Resolving conflicts between the effects of different networks is a major problem in design parameterization and information management.


