3.3: Advantage Loans Assignment
- Page ID
- 13025
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The purpose of this assignment is to:
1. Introduce the PMT function
2. Determine monthly payments
3. Determine total cost of a loan
4. Determine total interest to be paid
Preparation: (Review these terms)
- Arithmetic operators
- Wrap Text
- Setting up simple formulas
New Terms (Terms are bolded in the steps below)
- PMT Function (Step 10, page 2)
- How interest rates are presented (Step 10b, page 2)
- Insert a border around a table. (Step 14, Page 3)
Narrative:
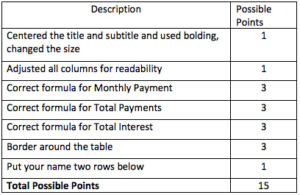
Having access to more money than you have in your pocket seems like a great deal. However, because it is someone else’s money they you are using, they charge you a fee – interest – to use it. When you see interest rates of 1.2% or 3.5% what does that actually mean in dollar and cents? Also the length of time you decide to pay back the loaned money affects the amount of dollars that you are paying back. This assignment will help you set up three different loans. After applying the PMT function and using some simple formulas, you will determine how much your loan is actually costing you. (THE ASSIGNMENT IS WORTH 15 POINTS. THE RUBRIC IS ON PAGE 4)
Advantage Loan Assignment
1. Open a blank spreadsheet
2. In A1 type Advantage Loans and Center it over the table. Make the font 14 pt.
3. Starting in A4, type in the labels (column headings) below in the appropriate cells:

4. Select B4 to H4 and click on Wrap Text in the HOME tab, Alignment Group. This will allow two rows in one cell in the header so the columns can stay narrow.
5. Starting in A5, type in these Lenders: Commercial Bank (A5), Credit Union (A6), Venture Capitalist (A7)
6. In B5-B7 type $153,000 for each Loan Amount.
7. Complete the worksheet as follows:
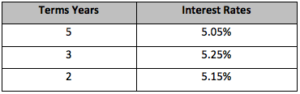
8. Note: when putting in the Interest Rates, use the percent sign or put the percentage into decimal form. If this isn’t done, the answers will be incorrect.
9. Use a formula to compute the Term Months (the number of months for each of the 3 lenders). In our example, the first bank – commercial bank- will loan the money for five years. How many months in a year? Create a formula in E5 which will compute the number of months for the loan. When this is completed, go to the next step.
10. Using PMT function. Click in cell F5. Next click on the FORMULA tab. From the Function Library find the category “Financial”. Scroll down the alphabetized list to find PMT. Below is the argument box that appears.
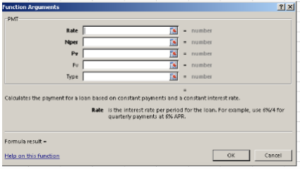
- Breakdown of the Arguments listed above.
RATE: Interest Rate Per Month. Be aware interest rates are given by the year!
NPER: Number of monthly payments
PV: Present Value
FV: Future Value and TYPE are not used for this formula.
- How interest rates are presented. Click in the box labeled Rate. Because interest rates are given for 12 months (one year), and because you are trying get a monthly rate, you need to divide the Interest Rate by 12 months. In the Argument box for rate, click on D5 (cell reference) for first interest rate and divide it by 12 (months in a year). The formula in the argument box should be D5/12. (You do not need to first use the equal sign because this is an argument box, not a cell that you are inputting a formula.)
- Next click in the box labeled NPER. This is asking for the number of monthly payments. You have already calculated that in Step 9 and the answer is in E5. So click on E5 for the NPER box.
- The PV or present value, is the amount of the loan. This is found in column A, the amount of the loan that you want. Click on B5.
- Click OK at the bottom of the argument box.
- Your answer will appear in F5. The answer will be in red. This represents the negative cash flow the loan represents to the borrower. To show the monthly payment as a positive number, place a minus sign in front of the PV cell reference or B5. The formula will look like this:=PMT(D5/12,E5,-B5). The commas represent the three separate boxes that you typed in cell references in the argument box.
11. Click in cell G5 for Monthly payment. The monthly payment will be the number of months (E5) times the monthly payment (F5). Type your formula in G5.
12. To determine the total interest, this would be the difference between the total payments and the actual amount of the loan being taken. Type your formula in H5.
13. Select the entire table from A1 to H7.
14. Insert a Border around a table.
- Click on HOME tab
- Look to the right for the Cells group. Click on Format.
- At the bottom of the pull down list, find the words ”Format Cells”. Click on it.
- This takes you to a dialog box. Click on the tab for Borders. Put a border around the outside of the table only – no inside lines.
15. Put your name two rows below the bottom of the table.
16. Re-Save his worksheet Advantage Loans. Submit the assignment through Blackboard.
17. If you are not in Blackboard, ask your teacher how to submit this assignment so that the formulas display.
Check the Rubric below to be sure you have completed all the tasks.
- Advantage Loans Assignment. Authored by: Fran Wells. License: CC BY: Attribution

