1.1: The Set of Real Numbers

Last updated
Save as PDF

Page ID: 20030

Kelly Brooks
Eastern Gateway Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The set of real numbers consists of the numbers that we use in everyday life. We will define the set of real numbers more precisely, but first, let’s define some other sets of numbers.

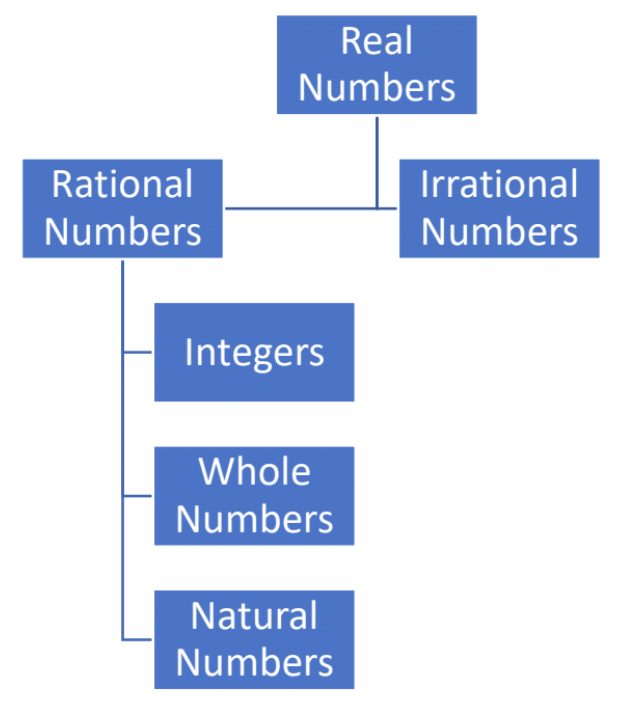
Natural Numbers: The counting numbers starting with 1: 1, 2, 3, 4, …

Whole Numbers: 0 and the counting numbers: 0, 1, 2, 3, 4, …

Integers: Positive and Negative Whole Numbers (includes 0); The whole numbers and their opposites: …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …

Rational Numbers: A number that can be written as a fraction (integers, terminating decimals and repeating decimals)

Irrational Numbers: Numbers that cannot be written as a fraction (non-terminating decimals and non-repeating decimals)

Real Numbers: All rational and irrational numbers

Some numbers can be classified in many categories. The next diagram displays the relationship between the different sets of numbers.

Example: Classify the following numbers

2.718
\(\sqrt{13}\)
\(\frac{24}{51} \)
101
\(0.\overline{3}\)
-5

See the video for the solutions.

The Real Number Line

We order real numbers on a number line based on their distance from 0. Positive numbers lie to the right of zero and Negative numbers lie to the left of zero. Each point on the number line corresponds to a real number.

Notice that -2 is represented by a distance of 2 units to the left of zero, the negative determines the side of zero while the 2 represents the distance from zero. Similarly, +2 is represented by a distance of 2 units to the right of zero, the positive indicates we move to the right of zero while the 2 represents the distance from zero. When writing positive numbers, it is customary not to write the “+” sign in the front.

Example: Plot the following numbers on a real number line

2.718
\(\sqrt{13}\)
\(\frac{24}{51}\)
101
\(0.\overline{3}\)
-5

See the video for a demonstration.

We determine the size of a number relative to another number using less than ((\<\)) or greater than (\(>\)) signs. Whichever number is further to the right, is larger, while a number that is further to the left is smaller.

We say “\(a\) is less than \(b\)” if \(a\) lies to the left of \(b\) on a real number line and we write this as: \(a < b\).

We say “\(a\) is greater than \(b\)” if \(a\) lies to the right of \(b\) on a real number line and we write this as: \(a >b\).

Examples: Use \(<\) or \(>\) to indicate the relationship between the stated numbers

7 ____ -3
5 ____ 12
5.8 ____ 5.7
-3.2 ____ -3.1
-5 ____ -12

See the video for the solutions.

The Opposite of a Number and Absolute Value

Definition: The opposite of a real number, \(a\), is \(-a\).

We can think of the opposite of a real number as changing the sign of the real number.

Examples: The opposite of 5 is -5. The opposite of -7 is – (-7) = 7

Hence, -(-7) can be read as “the opposite of -7” or “the opposite of the opposite of 7” or 7.

Definition: The absolute value of a real number is its distance from zero on a real number line. The notation for the absolute value uses two vertical bars on either side of the number, hence “the absolute value of a” would be denoted as \(\left|a\right|\). Since the absolute value represents a distance, its value is always positive.

Examples:

\(\left|5\right|\)= 5 since 5 is a distance of 5 from 0

\(\left|-7\right|\)=7 since -7 is a distance of 7 from 0