1.2: Mathematical Operations

The Addition of Integers and Decimals

Adding Numbers with the same signs

• Add the absolute values of the numbers and assign the common sign to the result
• NOTE: When the signs are both positive, add the values

Example: \(23+18\)

The common sign is +, so the answer will be positive, now we add the numbers to obtain

\[23+18=41\]

Example: \(-17+(-31)\)

The common sign is -, so the answer will be negative, now we add the absolute values of the numbers to obtain:

\[-17+\left( -31\right) =\]

First, calculate the sum of the absolute values:

\[\left|-17\right|+\left|-31\right|=\ 17+31=48\]

Next, assign the result the common sign, so the final answer is: -48.

\[-17+\left(-31\right)=-48\]

Adding Numbers with the Opposite Signs

• Take the absolute value of each number
• Subtract the smaller number from the larger number
• Assign the sign of the result based on the sign of the number with the larger absolute value
• NOTE: The sign of the larger absolute value wins. With practice, these steps will start to feel seamless.

Example: \(21+(-13)\)

First, calculate the absolute value of each number:

\[\left|21\right|=21 \text{ and } \left|-13\right|=13\]

Next, subtract the smaller number from the larger number:

\[21-13=8\]

Next, assign the sign of the number whose absolute value was greater, in this case, the sign of 21 is the sign of the final answer (positive), hence

\[21+\left(-13\right)=8\]

Scientific calculator keystrokes:

Example: \(28+(-54)\)

First, calculate the absolute value of each number:

\(\left|28\right|=28\) and \(\left|-54\right|=54\)

Next, subtract the smaller number from the larger number:

\[54-28=26\]

Next, assign the sign of the number whose absolute value was greater, in this case, the sign of -54 is the sign of the final answer (negative), hence

\[28+\left(-54\right)=-26\]

Short-cut: Now that we have gone through the formal process for adding integers, let’s get the general idea of the process:

• If the signs are the same, combine the numbers and keep the sign
• If the signs are different, disregarding the signs, subtract the smaller number from the larger number, then keep the sign of the larger number

Example: \(13+(-29)\)

Since 29 is larger than 13, we subtract 13 from 29 to get 16, and use the sign of 29 which is negative: -16

Example: \(-28+(-54)\)

Since the signs are the same, the answer will have the same sign (negative), now combine the numbers 28 + 54 = 82, so the final answer is -82

Similarly with decimal numbers:

Example: \(-2.34+\left(-5.4\right)=\)

Since the signs are the same, we add the numbers: 2.34 + 5.4 = 7.74 and keep the common sign (negative) to get – 7.74

Subtraction of Integers and Decimals

When subtracting an integer or decimal, we add the opposite of the number following the subtraction.

Example: \(15-7=\)

In this case, we can perform regular subtraction, however, we can also apply the subtraction rule of adding the opposite to obtain:

\[15+\left(-7\right)=8\]

since 15 is larger than 7, we subtract and keep the sign of the larger number which is positive

Example: \(3-12=\)

Remembering to add the opposite of 12, we get

\[3+\left(-12\right)=-9\]

Since the signs are different and 12 is larger than 3, we subtract \(12 -3\) to get 9, but use the sign of 12 which is negative to obtain -9

Likewise with decimal values:

Example: \(8.23-(-1.2)=\)

We first add the opposite of -1.2: \(8.23+1.2=\)

Next, we combine the numbers since they have same signs to obtain:

\[8.23-\left(-1.2\right)=8.23+1.2=9.43\]

Multiplication and Division of Integers and Decimals

To multiply or divide integers and decimals, we use multiply the numbers and use the following rules for the sign:

• If two numbers have the same signs, the result is positive
• If two numbers have different (opposite) signs, the result is negative

Examples:

1. \(\left(3\right)\left(-7\right)=\ -21\)
2. \(\left(-15\right)\left(-10\right)=150\)
3. \(\left(-5.2\right)\left(2\right)=-10.4\)
4. \(\left(2\right)\left(7\right)=14\)
5. \(\left(-25\right)\div \left(-5\right)=5\)
6. \(\left(-12.8\right)\div \left(4\right)=-3.2\)
7. \(\left(250\right)\div \left(-10\right)=-25\)
8. \(\left(48\right)\div \left(6\right)=8\)

Addition, Subtraction, Multiplication, and Division of Integers and Decimals using a Scientific Calculator

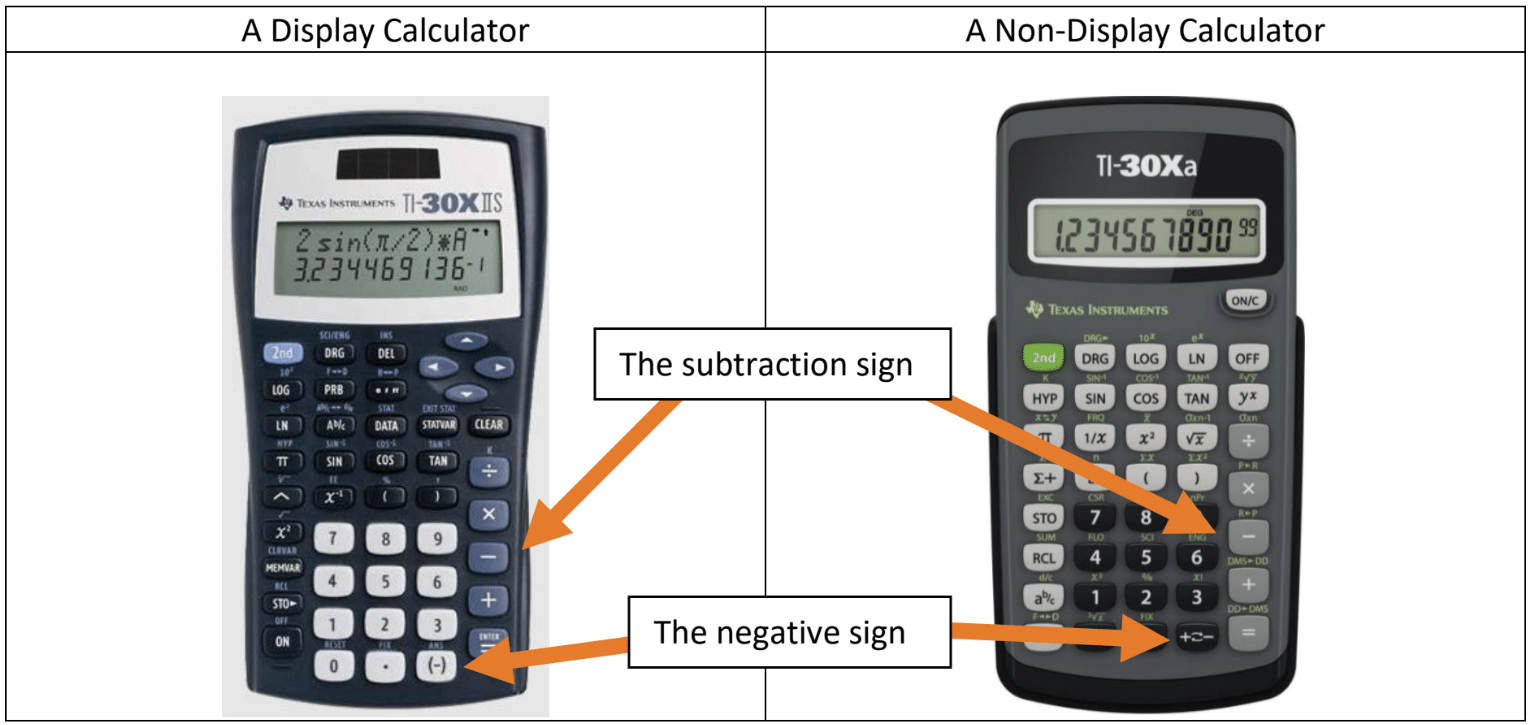
There are many types of scientific calculators available in the retail market, on our personal computers, and even on our personal devices such as cell phones and tablets. As a result, let’s first distinguish between two types of scientific calculators: A Display calculator and a non-display calculator. Some examples of display calculators are: TI30XIIS, TI-36X Pro, TI-30XS Multiview, and the Casio fx-350ES PLUS. Some examples of non-display calculators are TI-30Xa, most cell phone calculators, and most calculators on personal computers.

For our purposes, we will determine if a calculator is a “Display” calculator or a “non-display” calculator by doing the following:

Type 2 + 3 on your calculator.

• If your screen displays the entire expression 2 + 3, then you have a “Display” calculator.
• If you screen displays only the 3 after typing 2 + 3, then you have a “non-display” calculator.

On Display calculators, we can usually enter the problem as it is written. On a non-display calculator, we usually must enter the problem in reverse order of operations (see Unit 2 for more information).

Let’s revisit some of our earlier examples and calculate them on the scientific calculator. For negative numbers, be sure to use the negative symbol, (-), which is generally at the bottom of the keyboard on a TI calculator and not the subtraction symbol, -, which is usually on the right side of the keyboard. Each calculator is different, so you may have to experiment with your calculator to determine the process.

To compute -17+(-31) use the following sequence of keystrokes to obtain -48:

Display Calculator:	Non-display Calculator:
(-) 17 + (-) 31 ENTER	17 (-) + 31 (-)=
Type the negative sign before the number	Type the negative number after the sign

To compute 8.23-(-1.2)= use the following sequence of keystrokes to obtain 9.43:

Display Calculator	Non-display Calculator:
8.23 - (-) 1.2 ENTER	8.23 - 1.2 (-) =
Use the subtraction key, then type the negative sign before the number	Use the subtraction key then type the negative sign after the number

To compute (-15)(-10) = use the following sequence of keystrokes to obtain 150:

Display Calculator	Non-display Calculator:
(-)15 X (-)10 ENTER	15 (-) X 10 (-) =
Type the negative sign before the number	Type the negative sign after the number

To compute (250)\(\div\)(-10) = use the following sequence of keystrokes to obtain -25:

Display Calculator	Non-display Calculator:
250\(\div\)(-)10 ENTER	250\(\div\)10(-) =
Type the negative sign before the number	Type the negative sign after the number

Fractions

Fractions are real numbers that indicate a portion of a whole. A fraction consists of a numerator and denominator. The denominator represents the number of equal parts of an object and the numerator represents a portion of those equal parts. For example, if pipe is separated into 4 equal parts, ¼ would represent 1 out of 4 of the parts, 2/4 would represent 2 out of the 4 parts, ¾ would represent 3 out of the 4 parts, and 4/4 = 1 would represent all 4 parts or the whole pipe. Likewise, 0/4 would represent 0 of the 4 parts or nothing, hence 0/4 = 0.

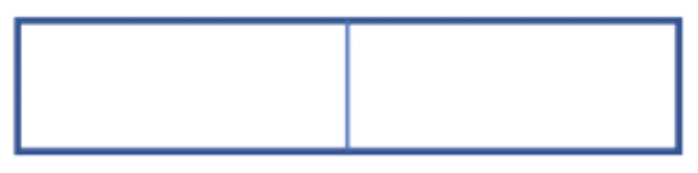
The rectangle below is divided into two equal parts. Hence 1 of the pieces out of the 2 pieces would represent 1/2.

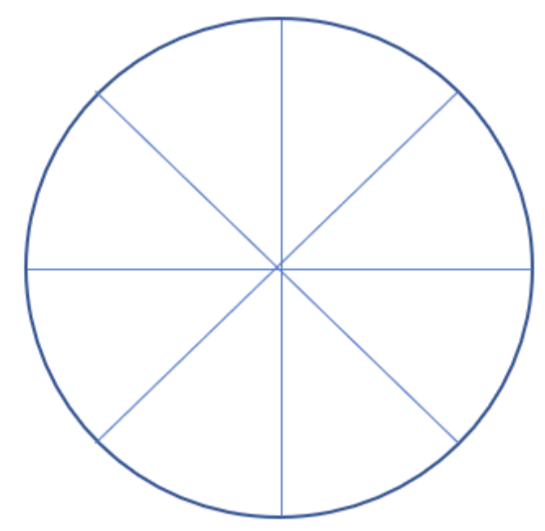
The circle shown below is divided into 8 equal parts. 1 part would represent 1/8. 2 parts would represent 2/8 which would reduce to ¼ for a couple of reasons:

1. if we were to shade 2 of the 8 pieces, that would also represent 1 of 4 equal pieces and
2. 2/8 can be reduced by dividing both the numerator (2) and the denominator (8) by the same number, which in this case would be 2, hence: \(\frac{2}{8}=\frac{2\div 2}{8\div 2}=\frac{1}{4}\)

The “bar” in a fraction also represents division, so ¼ would also mean \(1\div 4\). This can be interpreted as a whole divided into 4 equal parts or 1 of 4 equal parts.

Fractions have many applications. Fractions can also be used to represent units such as miles per hour or \(\frac{miles}{hour}\). Fractions can also be used to denote ratios and proportions; we will see the use of fractions in these applications in a later unit.

Multiplying and Dividing Fractions

To multiply fractions:

Multiply the numerators and multiply the denominators.

To simplify, reduce by dividing like factors (numbers that divide into other numbers).

Examples:

1. \(\frac{2}{3}\cdot \frac{5}{7}\)

a. Multiply the numerators and multiply the denominators.

\[\frac{2}{3}\cdot \frac{5}{7}=\frac{10}{21}\nonumber \]

Since 10 and 21 do not have any common factors, this is the simplified or reduced answer.

2. \(\frac{22}{63}\cdot \frac{9}{24}\)

a. Multiply the numerators and multiply the denominators.

\[\frac{22}{63}\cdot \frac{9}{24}=\frac{108}{1512}\nonumber \]

b. Simplify by reducing the fraction (divide the numerator and denominator by the same number(s))

\[\frac{108}{1512}=\frac{108\div 12}{1512\div 12}=\frac{9}{126}=\frac{9\div 9}{126\div 9}=\frac{1}{14}\nonumber \]

Another option for this problem is to reduce before multiplying:

\[\frac{12}{63}\cdot \frac{9}{24}\nonumber \]

a. Reduce the numerators and denominators by dividing each by the same number

\[\frac{12\div 12}{63\div 9}\cdot \frac{9\div 9}{24\div 12}=\frac{1}{7}\cdot \frac{1}{2}\nonumber \]

b. Multiply the numerators and denominators (multiply straight across)

\[\frac{1}{7}\cdot \frac{1}{2}=\frac{1}{14}\nonumber \]

3. \(\frac{24}{72}\cdot \frac{18}{30}\)

Since the numbers in the fractions are large, let’s reduce first, then multiply.

Determine numbers that divide into both the numerator and denominator:

9 divides into 18 and 72; 6 divides into 24 and 30 OR 6 divides into 18 and 30; 24 divides into 24 and 72

\[\frac{24}{72}\cdot \frac{18}{31}=\frac{24\div 6}{72\div 9}\cdot \frac{18\div 9}{30\div 6}=\frac{4}{8}\cdot \frac{2}{5}=\frac{4\div 4}{8\div 4}\cdot \frac{2}{5}=\frac{1}{2}\cdot \frac{2}{5}=\frac{1}{2\div 2}\cdot \frac{2\div 2}{5}=\frac{1}{5} \nonumber \]

OR

\[\frac{24}{72}\cdot \frac{18}{31}=\frac{24\div 24}{72\div 24}\cdot \frac{18\div 6}{30\div 6}=\frac{1}{3}\cdot \frac{3}{5}=\frac{1}{3\div 3}\cdot \frac{3\div 3}{5}=\frac{1}{5} \nonumber \]

To divide fractions: Invert the second fraction and change the operation to multiplication and continue as described above.

Example: \(\frac{3}{5}\div \frac{9}{10}\)

\[\frac{3}{5}\div \frac{9}{10}= \frac{3}{5}\cdot \frac{10}{9}=\frac{30}{45}=\frac{2}{3}\nonumber \]

Example: \(\frac{15}{7}\div \frac{25}{21}\)

\[\frac{15}{7}\div \frac{25}{21}=\frac{15}{7}\cdot \frac{21}{25}=\frac{3}{1}\cdot \frac{3}{5}=\frac{9}{5}\nonumber \]

Adding and Subtracting Fractions

With like denominators

To add or subtract fractions, the fractions must have the same denominator:

Step 1: Verify that the fractions are like fractions (fractions with the same denominator).

Step 2: Add or subtract the numerators and keep the same denominator.

Examples:

1. \(\frac{2}{7}+\frac{3}{7}=\frac{2+3}{7}=\frac{5}{7}\)
2. \(\frac{14}{17}-\frac{5}{17}=\frac{14-5}{17}=\frac{9}{17}\)

With unlike Denominators

Step 1: Rewrite the unlike fractions (fractions with different denominators) as like fractions (fractions with the same denominator) with the least common multiple as their new denominator. This new denominator is called the least common denominator (LCD).

To determine the least common denominator (LCD), find the smallest common multiple of the denominators, in other words, find the smallest number that both denominators divide into

Rewrite the unlike fractions as like fractions by multiplying the numerator and denominator of each fraction by the number that makes the denominator of each the least common denominator.

Step 2: Add or subtract the numerators and keep the common denominator.

Examples:

1. \(\frac{2}{3}+\frac{1}{9}=\)

First find the smallest number that both 3 and 9 will divide into, in this case it will be 9, so 9 is the LCD.

So, we need to multiply the first fraction by 3/3 to create a 9 in the denominator:

\[\frac{3}{3}\cdot \frac{2}{3}+\frac{1}{9}=\frac{6}{9}+\frac{1}{9}=\frac{7}{9}\nonumber \]

2. \(\frac{3}{7}+\frac{1}{4}=\)

The least common denominator = 28 (since 28 is the smallest number that can be divided by both 7 and 4)

Next, multiply the numerator and denominator of 3/7 by 4/4 to create a denominator of 28 and multiply the numerator and denominator of ¼ by 7/7 to create a denominator of 28, finally add the numerators and keep the common denominator.

\[\frac{4}{4}\cdot \frac{3}{7}+\frac{1}{4}\cdot \frac{7}{7}=\frac{12}{28}+\frac{7}{28}=\frac{19}{28}\nonumber \]

NOTE: We add, subtract, multiply, and divide negative fractions similar to how we added, subtracted, multiplied and divided negative numbers in Section ___.

Percents

A percent is defined to be an amount based on 100. If we divide the word into two words, we have “per” and “cent”. Per means divide by and cent means 100, hence divide by 100 or out of 100.

Example: 54% means 54 out of 100

We will use percentages to calculate values in Unit ____.

Converting between different types of numbers (fractions, decimals, and percentages)

To convert from a fraction to a decimal, divide the numerator by the denominator.

To convert from a decimal to a fraction, determine the place of the last digit after the decimal, write the fraction as all the digits after the decimal over the last place of the decimal.

Example: 0.547 represents 547 thousandths since the last digit after the decimal is in the thousandths place, we have 547/1000.

To convert from a fraction to a percent

Option 1: Convert the fraction to a decimal, then convert the decimal to a percent

Option 2: Use a proportion to write the fraction with a denominator of 100, then using the definition of a percent, the percent will be based on the numerator of the fraction with a denominator of 100. We will explore this option more in Unit ___ when we learn about proportions.

To convert from a decimal to a percent, multiply the decimal by 100 or move the decimal place two units to the right.

To convert from a percent to a decimal, divide the percent number by 100 or move the decimal place two units to the left.